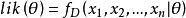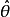最大似然估計

最大似然估計(maximum likelihood estimation, MLE)一種重要而普遍的求估計量的方法。最大似然法明確地使用機率模型，其目標是尋找能夠以較高機率產生觀察數據的系統發生樹。最大似然法是一類完全基於統計的系統發生樹重建方法的代表。

基本介紹

• 中文名：最大似然估計
• 外文名：Maximum Likelihood Estimate
• 英文簡寫：MLE
• 本質：統計方法
• 使用工具：機率模型
• 套用學科：統計學

概述

最大似然估計是一種統計方法，它用來求一個樣本集的相關機率密度函式的參數。這個方法最早是遺傳學家以及統計學家羅納德·費雪爵士在1912年至1922年間開始使用的。

“似然”是對likelihood 的一種較為貼近文言文的翻譯，“似然”用現代的中文來說即“可能性”。故而，若稱之為“最大可能性估計”則更加通俗易懂。

最大似然法明確地使用機率模型，其目標是尋找能夠以較高機率產生觀察數據的系統發生樹。最大似然法是一類完全基於統計的系統發生樹重建方法的代表。該方法在每組序列比對中考慮了每個核苷酸替換的機率。

例如，轉換出現的機率大約是顛換的三倍。在一個三條序列的比對中，如果發現其中有一列為一個C，一個T和一個G，我們有理由認為，C和T所在的序列之間的關係很有可能更接近。由於被研究序列的共同祖先序列是未知的，機率的計算變得複雜；又由於可能在一個位點或多個位點發生多次替換，並且不是所有的位點都是相互獨立，機率計算的複雜度進一步加大。儘管如此，還是能用客觀標準來計算每個位點的機率，計算表示序列關係的每棵可能的樹的機率。然後，根據定義，機率總和最大的那棵樹最有可能是反映真實情況的系統發生樹。

原理

給定一個機率分布D，假定其機率密度函式（連續分布）或機率聚集函式（離散分布）為f_D，以及一個分布參數θ，我們可以從這個分布中抽出一個具有n個值的採樣X₁,X₂,...,X_n，通過利用f_D，我們就能計算出其機率：

但是，我們可能不知道θ的值，儘管我們知道這些採樣數據來自於分布D。那么我們如何才能估計出θ呢？一個自然的想法是從這個分布中抽出一個具有n個值的採樣X₁,X₂,...,X_n，然後用這些採樣數據來估計θ。

一旦我們獲得，我們就能從中找到一個關於θ的估計。最大似然估計會尋找關於 θ的最可能的值（即，在所有可能的θ取值中，尋找一個值使這個採樣的“可能性”最大化）。這種方法正好同一些其他的估計方法不同，如θ的非偏估計，非偏估計未必會輸出一個最可能的值，而是會輸出一個既不高估也不低估的θ值。

要在數學上實現最大似然估計法，我們首先要定義可能性：

並且在θ的所有取值上，使這個函式最大化。這個使可能性最大的值即被稱為θ的最大似然估計。

性質

泛函不變性（Functional invariance）

如果 是 θ的一個最大似然估計，那么α =g(θ)的最大似然估計是 。函式g無需是一個——映射。

漸近線行為

最大似然估計函式在採樣樣本總數趨於無窮的時候達到最小方差（其證明可見於Cramer-Rao lower bound）。當最大似然估計非偏時，等價的，在極限的情況下我們可以稱其有最小的均方差。對於獨立的觀察來說，最大似然估計函式經常趨於常態分配。

偏差

最大似然估計的非偏估計偏差是非常重要的。考慮這樣一個例子，標有1到n的n張票放在一個盒子中。從盒子中隨機抽取票。如果n是未知的話，那么n的最大似然估計值就是抽出的票上標有的n，儘管其期望值的只有(n + 1) / 2。 為了估計出最高的n值，我們能確定的只能是n值不小於抽出來的票上的值。

最大似然估計的一般求解步驟

基於對似然函式L(θ)形式(一般為連乘式且各因式>0)的考慮，求θ的最大似然估計的一般步驟如下：

(1)寫出似然函式

總體X為離散型時：

總體X為連續型時：

(2)對似然函式兩邊取對數有

總體X為離散型時：

總體X為連續型時：

(3)對 求導數並令之為0：

此方程為對數似然方程。解對數似然方程所得，即為未知參數 的最大似然估計值。

例題

設總體X~N(μ，σ²)，μ，σ為未知參數，X1,X2...,Xn是來自總體X的樣本，X1,X2...,Xn是對應的樣本值，求μ與σ²的最大似然估計值。

解：X的機率密度為

可得似然函式如下：

取對數，得

令

解得

故μ和σ的最大似然估計量分別為