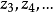有限信息最大似然法(LIML)是求過度識別方程式的結構參數的一致估計量的一種單方程估計方法。用它來估計方程時，通常先將結構式方程化為簡單式方程，然後求結構式參數和簡化式參數的關係，建立似然函式，最後求出參數的有限信息最大似然估計量。此方法得到的參數估計量是有偏的，但是一致的。
基本介紹
- 中文名：有限信息最大似然法
- 外文名：LIML (limited information maximum likelihood method)
- 所屬學科：數學
- 屬性：估計單一結構式參數的方法
- 相關概念：最大似然法等
基本介紹,相關分析,
基本介紹
有限信息最大似然法指在只考慮所估計方程的約束的前提下，用最大似然法估計結構方程的參數。有限信息最大似然法是一種單方程估計法，它適用於過度識別的方程系統。這種方法通常是先將結構式方程化為簡化式方理，然後求結構式參數和簡化式參數的關係，建立似然的數，最後求似然函式在約束條件下的極大似然值。
有限信息最大似然法，可以說是FIML的簡化。它只考慮部分結構式所提供的有限信息，然後利用最大似然法。它屬於估計單一結構式參數的又一方法。所得估計量具有一致性。隨機項滿足常態分配的話則具有漸近有效的大樣本特性。在計算上比FIML簡單些，但仍然較繁雜。
相關分析
有限信息最大似然法是對聯立方程式體系中的每一個方程式運用最大似然法求參數估計值的一種方法。在採用這一方法的時候，是將有關包含於方程式體系中的先決變數的信息作為約束條件，在此基礎上進行最大似然估計。
現在，在聯立方程式體系中使用k個先決變數，而有p個先決變數存在於想要估計的個別方程式之中(
)，因此，想要估計的方程式里沒有包含的先決變數就有(k-p)個。在這種場合。可把這(k-p)個先決變數的參數解釋為“0”。這就叫做“零係數約束”。(實際上，聯立方程式體系里也包含了內生變數是相互關連的這一信息。但在有限信息最大似然法的場合，卻無視這點。在這個意義上來說，並沒有完全利用該體系所具有的全部信息。這就是“有限信息”的來由)。
為了理解有限信息最大似然法，我們稍梢改變一下思路，導入“最小方差比”這一概念。
現在，假定想估計的方程式如下：
式中，
表示內生變數，
表示先決變數。
這裡將對兩種情形加以比較。一種情形是將內生變數的線性組合
對體系內的所有先決變數進行回歸，另一種情形是將僅對方程式所含的先決變數
進行回歸。如果前提是該方程僅含
與
(其它先決變數的參數為0：零係數約束)的先驗判斷是正確的，則上述兩種場合下的方程式之解釋能力不會有多大差別(就是說，即使把與之外的先決變數
也加到解釋變數之中，也不能提高方程式的解釋能力)。 ·
於是，可以考慮方差比
用與回歸
時的殘差之方差/用全部先決變數回歸時的殘差之方差，並決定的權重和的參數，以使
為最小(這與在認為
的情況下使接近於
的場合是一致的)。
這樣求得的估計量就叫做“最小方差比估計量”。這種估計量在結果上與用有限信息最大似然法求得的“有限信息最大似然估計量”是一致的。
另外，有限信息最大似然估計量是一致估計量，在數據充分多的場合，這一估計量與用二階段最小二乘法求得的估計量是一致的。
