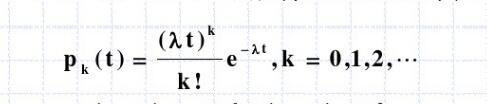隨機變數分為離散型隨機變數與 非離散型隨機變數兩種,隨機變數的函式仍為隨機變數。有些隨機變數,它全部可能取到的不相同的值是有限個或可列無限多個,也可以說機率1以一定的規律分布在各個可能值上。這種隨機變數稱為"離散型隨機變數"。
基本介紹
- 中文名:離散性隨機變數
- 外文名:discrete random variable
- 重要分布:0-1分布、泊松分布、超幾何分布
- 取值:可數、可列
- 套用領域:信號與系統
- 對比:連續性隨機變數
主要區別
機率分布
定義1
定義2
性質
內容
釋義
P{X∈A}=∑Pn
特別的,如果一個試驗所包含的事件只有兩個,其機率分布為
P{X=x1}=p(0<p<1)
P{X=x2}=1-p=q
這種分布稱為兩點分布。 如果x1=1,x2=0,有
P{X=1}=p
P{X=0}=q
這時稱X服從參數為p的0-1分布,它是離散型隨機變數分布中最簡單的一種。由於是數學家伯努利最先研究發現的,為了紀念他,我們也把服從這種分布的試驗叫伯努利試驗。習慣上,把伯努利的一種結果稱為“成功”,另一種稱為“失敗”。
隨機變數
X | 0 | 1 |
P | 1-p | p |