基本介紹
- 中文名:數學期望值
- 外文名:Mathematical expectation value
- 簡稱:期望
- 所屬領域:機率論;統計學
簡介

數學定義








性質


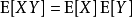
期望值的運用













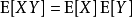

在機率論和統計學中,一個離散性隨機變數的數學期望值(或數學期望、或均值,亦簡稱期望,物理學中稱為期待值)是試驗中每次可能的結果乘以其結果機率的總和。...
在機率論和統計學中,數學期望(mean)(或均值,亦簡稱期望)是試驗中每次可能結果的機率乘以其結果的總和,是最基本的數學特徵之一。它反映隨機變數平均取值的大小。...
在機率論和統計學中,期望值(或數學期望、或均值,亦簡稱期望,物理學中稱為期待值)是指在一個離散性隨機變數試驗中每次可能結果的機率乘以其結果的總和。換句話說...
中文名稱 [數學]期望 英文名稱 mathematical expectation 定義 一次隨機抽樣中所期望的某隨機變數的取值。 套用學科 遺傳學(一級學科),群體、數量遺傳學(二級學科...
方差是在機率論和統計方差衡量隨機變數或一組數據時離散程度的度量。機率論中方差用來度量隨機變數和其數學期望(即均值)之間的偏離程度。統計中的方差(樣本方差)是...
若隨機變數X服從一個數學期望為μ、方差為σ^2的常態分配,記為N(μ,σ^2)。其機率密度函式為常態分配的期望值μ決定了其位置,其標準差σ決定了分布的幅度。...
均方值方差:偏差: 所以方差也稱為偏差的均方值。對於隨時間連續變化的一個變數x(也可看時 ),其數學期望可寫成:它實際上就是 的平均值 。...
平均成績相同,但X 不穩定,對平均值的偏離大。方差描述隨機變數對於數學期望的偏離程度。單個偏離是消除符號影響方差即偏離平方的均值,記為D(X):直接計算公式分離散...
無偏估計是用樣本統計量來估計總體參數時的一種無偏推斷。估計量的數學期望等於被估計參數的真實值,則稱此此估計量為被估計參數的無偏估計,即具有無偏性,是一...
有:指數分布數學期望 編輯 期望值:比方說:如果你平均每個小時接到2次電話,那么你預期等待每一次電話的時間是半個小時。指數分布方差 編輯 ...
因此,上式可以成為一個分布列,此分布列是兩個幾何數列一般項的和,在這裡稱X服從兩事件下推廣的幾何分布,記為X ~ PGE(2;p) ,數學期望為: 。當P = 時,E...
機率論歷史上第一個極限定理屬於伯努利,後人稱之為“大數定律”。機率論中討論隨機變數序列的算術平均值向隨機變數各數學期望的算術平均值收斂的定律。在隨機事件的...
,它的各個分量是自旋沿著各坐標軸分量的數學期望值,即 。這個矢量描述自旋所指的“方向”,對應於經典物理下旋轉軸的概念。這個矢量在實際做量子力學計算時並不十分...
