定義
機率密度函式
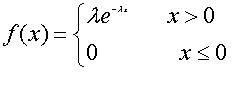 公式
公式其中λ > 0是分布的一個參數,常被稱為率參數(rate parameter)。即每單位時間內發生某事件的次數。指數分布的
區間是[0,∞)。 如果一個
隨機變數X呈指數分布,則可以寫作:
X~ E(λ)。
在不同的教材有不同的寫法,θ=1/λ,因此機率密度函式,
分布函式和
期望方差有兩種寫法。
其中θ>0為常數,則稱X服從參數θ的指數分布。
分布函式
指數分布的分布函式由下式給出:
有:
數學期望
比方說:如果你平均每個小時接到2次電話,那么你預期等待每一次電話的時間是半個小時。
方差
記號
特性
無記憶性
指數函式的一個重要特徵是無記憶性(Memoryless Property,又稱遺失記憶性)。這表示如果一個隨機變數呈指數分布
即,如果T是某一元件的壽命,已知元件使用了t小時,它總共使用至少
小時的條件機率,與從開始使用時算起它使用至少s小時的機率相等。
分位數
參數λ的四分位數函式(Quartile function)是:
分布
在
機率論和統計學中,指數分布(Exponential distribution)是一種
連續機率分布。指數分布可以用來表示獨立
隨機事件發生的時間間隔,比如旅客進機場的時間間隔、
中文維基百科新條目出現的時間間隔等等。
許多電子產品的壽命分布一般服從指數分布。有的系統的壽命分布也可用指數分布來近似。它在可靠性研究中是最常用的一種分布形式。指數分布是
伽瑪分布和
威布爾分布的特殊情況,產品的失效是偶然失效時,其壽命服從指數分布。
指數分布可以看作當威布爾分布中的形狀係數等於1的特殊分布,指數分布的失效率是與時間t無關的常數,所以分布函式簡單。
套用
在電子元器件的可靠性研究中,通常用於描述對發生的缺陷數或系統故障數的測量結果。這種分布表現為
均值越小,分布偏斜的越厲害。
指數分布套用廣泛,在日本的工業標準和美國軍用標準中,半導體器件的抽驗方案都是採用指數分布。此外,指數分布還用來描述大型
複雜系統(如計算機)的
平均故障間隔時間MTBF的失效分布。但是,由於指數分布具有缺乏“記憶”的特性.因而限制了它在機械可靠性研究中的套用,所謂缺乏“記憶”,是指某種產品或零件經過一段時間t0的工作後,仍然如同新的產品一樣,不影響以後的工作壽命值,或者說,經過一段時間t0的工作之後,該產品的壽命分布與原來還未工作時的壽命分布相同,顯然,指數分布的這種特性,與機械零件的疲勞、磨損、腐蝕、蠕變等損傷過程的實際情況是完全矛盾的,它違背了產品損傷累積和老化這一過程。所以,指數分布不能作為機械零件功能參數的分布形式。
指數分布雖然不能作為機械零件功能參數的分布規律,但是,它可以近似地作為高可靠性的複雜部件、機器或系統的失效分布模型,特別是在部件或機器的整機試驗中得到廣泛的套用。
指數分布的圖形表面上看與冪律分布很相似,實際兩者有極大不同,指數分布的收斂速度遠快過冪律分布。
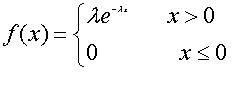 公式
公式




















