基本介紹
- 中文名:拉普拉斯分布
- 外文名:The Laplace distribution
- 提出:拉普拉斯
- 發現時間:1774年
- 領域:數學
- 性質:指數分布
- 參數:位置參數,尺度參數
定義,拉普拉斯分布的若干性質,套用,
定義
設隨機變數 具有密度函式
具有密度函式


其中 為常數,且
為常數,且 ,則稱
,則稱 服從參數為
服從參數為 的拉普拉斯分布。
的拉普拉斯分布。




易見, ,且
,且 ,
,


(令 ) =
) = .
.


可見

此外


拉普拉斯分布的若干性質

則稱X服從參數為 (位置參數)和
(位置參數)和 (尺度參數)的拉普拉斯(Laplace)分布,記作
(尺度參數)的拉普拉斯(Laplace)分布,記作 .
.



2.設 ,則它的分布函式為
,則它的分布函式為 .
.


3.設 ,則
,則 .
.


4..設 ,則它的r階中心矩為
,則它的r階中心矩為 當r為奇數是其值為0,為偶數時其值為
當r為奇數是其值為0,為偶數時其值為 。
。



5.設 ,則
,則



套用
在近代統計中,穩健性占有重要的地位,例如在古典回歸分析中,用偏差平方和的大小作標準,來選擇回歸係數使它達到極小,這種回歸不具有穩健性,然而,如改為用偏差的絕對值和作為標準,卻具有穩健性.。於是研究隨機變數絕對值的分布是很有意義的. 設 ,可以證明
,可以證明 ,其中
,其中 這是一個很有意思的結果。若X與Y獨立同分布於
這是一個很有意思的結果。若X與Y獨立同分布於 ,則
,則 ,上述兩個事實表明,若在回歸分析中假定服從拉普拉斯分布,並用絕對偏差和作為標準,可以導出很多良好的性質。
,上述兩個事實表明,若在回歸分析中假定服從拉普拉斯分布,並用絕對偏差和作為標準,可以導出很多良好的性質。





拉普拉斯分布與常態分配有一定的聯繫。 設 X , Y , Z ,W 獨立同分布於N(0,1),則

拉普拉斯分布和哥西分布之間有著非常有趣的聯繫。C (0,1) 的分布密度和特徵函式 分別為

而 的分布密度和持征函式分別是
的分布密度和持征函式分別是


設 是總體
是總體 的樣本,欲通過它們來估計
的樣本,欲通過它們來估計 和
和 ,將
,將 重排得
重排得 ,若n為奇數,用
,若n為奇數,用 作為
作為 的估計;若n為偶數,則可用
的估計;若n為偶數,則可用 至
至 之間的任何一個數來作為
之間的任何一個數來作為 的估計,通常用
的估計,通常用












而 的估計是:
的估計是:

若 已知,則
已知,則


若 未知,則
未知,則


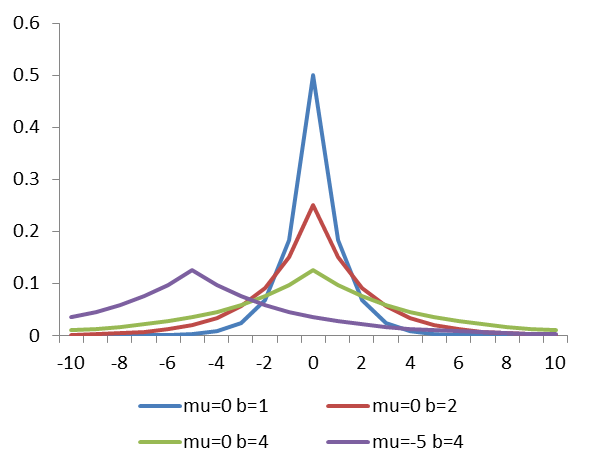

 拉普拉斯分布的密度曲線
拉普拉斯分布的密度曲線





