拉普拉斯中心極限定理也稱棣莫弗-拉普拉斯中心極限定理,它是關於二項分布漸近趨於常態分配的極限定理,因此,也稱二項分布的中心極限定理,拉普拉斯中心極限定理是獨立同分布中心極限定理(林德貝格-勒維中心極限定理)的特例。
基本介紹
- 中文名:拉普拉斯中心極限定理
- 提出者:棣莫弗、拉普拉斯
- 套用學科:機率論

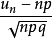

定理
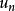




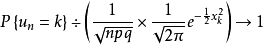



含義

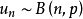
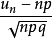


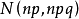
套用
用頻率估計機率時的計算問題

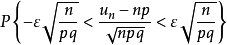

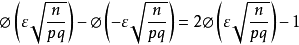
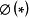
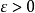

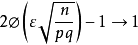
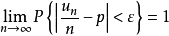

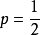
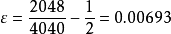
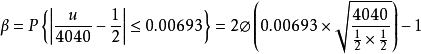
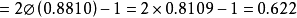
拉普拉斯中心極限定理也稱棣莫弗-拉普拉斯中心極限定理,它是關於二項分布漸近趨於常態分配的極限定理,因此,也稱二項分布的中心極限定理,拉普拉斯中心極限定理是獨立同分布中心極限定理(林德貝格-勒維中心極限定理)的特例。

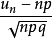

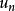




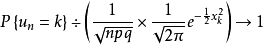




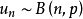
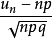


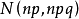

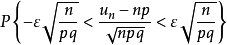

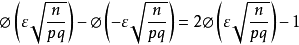
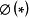
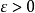

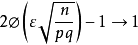
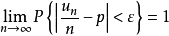

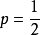
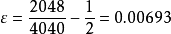
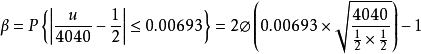
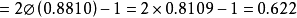
拉普拉斯中心極限定理也稱棣莫弗-拉普拉斯中心極限定理,它是關於二項分布漸近趨於常態分配的極限定理,因此,也稱二項分布的中心極限定理,拉普拉斯中心極限定理是獨立同...
中心極限定理,是指機率論中討論隨機變數序列部分和分布漸近於常態分配的一類定理。這組定理是數理統計學和誤差分析的理論基礎,指出了大量隨機變數近似服從常態分配的...
棣莫弗—拉普拉斯中心極限定理(De Moivre-Laplace),即二項分布以常態分配為其極限分布定律。...
棣莫弗一拉普拉斯局部極限定理(De Moivre-Laplace local limit theorem)是關於伯努利試驗的極限定理。伯努利試驗(Bernoulli experiment)是在同樣的條件下重複地、相互...
隸莫佛-拉普拉斯定理給出了二項分布的近似計算公式。...... 在機率論的中心極限定理中隸莫佛-拉普拉斯定理給出了二項分布的近似計算公式。隸莫佛-拉普拉斯定理的主...
德莫佛對數學最著名的貢獻是德莫佛公式(de Moivre Formula)和德莫佛-拉普拉斯中心極限定理,以及他對常態分配和機率理論的研究。德莫佛還寫了一本機率理論的教科書,The...
⒉棣莫弗的工作對數理統計學最大的影響,當然還在於現今以他的名字命名的中心極限定理。棣莫弗做出他的發現後約40年,拉普拉斯建立了中心極限定理較一般的形式,獨立...
第五章:大數定律和中心極限定理考試內容切比雪夫(Chebyshev)不等式切比雪夫大數定律伯努利(Bernoulli)大數定律辛欽(Khinchine)大數定律 棣莫弗-拉普拉斯(De Moivre-...
2.了解棣莫弗—拉普拉斯中心極限定理(二項分布以常態分配為極限分布)、列維—林德伯格中心極限定理(獨立同分布隨機變數序列的中心極限定理),並會用相關定理近似計算...
5.2中心極限定理 5.2.1獨立同分布中心極限定理 5.2.2棣莫弗—拉普拉斯中心極限定理 本章小結 習題5 第6章數理統計的基本概念 6.1幾個基本概念 6.1.1總體...
第二節 二維隨機變數的函式第三節 服從同-零-壹分布的相互獨立隨機變數的和 隸莫佛-拉普拉斯(De Moivre-Laplace)中心極限定理習題七第八章 隨機變數的數字特徵...
第二節 中心極限定理 89一、獨立同分布中心極限定理 90二、棣莫弗-拉普拉斯中心極限定理 91習題五 93第六章 數理統計的基礎知識 95...
