基本介紹
- 中文名:雙指數分布
- 外文名:Laplace distribution
- 作用領域:保險與精算
- 分布範圍:非常廣泛
- 主要作用:建立各種經濟模型。
機率分布、機率密度以及分位數函式,生成拉普拉斯變數,相關分布,
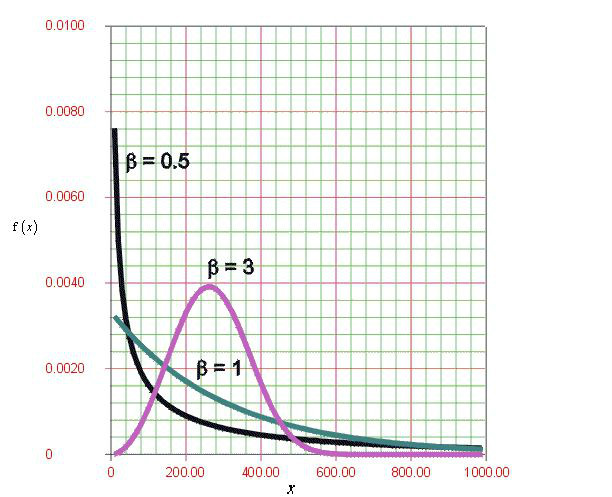
在機率論與統計學中,拉普拉斯分布是以皮埃爾-西蒙·拉普拉斯的名字命名的一種連續機率分布。由於它可以看作是兩個不同位置的指數分布背靠背拼接在一起,所以它也叫作...
車輛到達數、停靠數常用離散型的泊松分布、二項分布、負二項分布、歐蘭分布等;描述車頭時距和車速常用連續型的常態分配、負指數分布、移位負指數分布、雙指數分布...
[55] 丁曉, 韋來生, 雙指數分布位置參數經驗Bayes估計問題. 數學雜誌,25 (4),2005,413-420.[56] Wei Laisheng and Wang Lichun , Empirical Bayes estimation...
極值分布在氣候正常時用的是I型極值分布(又稱雙指數分布)原始分布屬指數型,其極大值X的分布應屬I型分布,其分布函式:檢驗風速的理論分布與經驗分布的適合度,一般...
Double exponential distribution, 雙指數分布Double logarithmic, 雙對數Downward rank, 降秩Dual-space plot, 對偶空間圖DUD, 無導數方法...
例6 均勻分布(連續均勻分布)例7 三角形分布例8 最小極值和最大極值分布例9 Beta分布例10 Gamma分布(Erlang分布)例11 Laplace分布(雙指數分布)...
