物理學現象 定義 被分子撞擊的懸浮微粒做無規則運動的現象叫做布朗運動。布朗運動是將看起來連成一片的液體,在高倍顯微鏡下看其實是由許許多多分子組成的。液體分子不停地做無規則的運動,不斷地隨機撞擊懸浮微粒。當懸浮的微粒足夠小的時候,由於受到的來自各個方向的液體分子的撞擊作用是不平衡的。在某一瞬間,微粒在另一個方向受到的撞擊作用超強的時候,致使微粒又向其它方向運動,這樣就引起了微粒的無規則的運動,即布朗運動。
例如,在顯微鏡下觀察懸浮在水中的藤黃粉、花粉微粒,或在無風情形觀察空氣中的煙粒、塵埃時都會看到這種運動。溫度越高,運動越激烈。它是1827年植物學家R.布朗最先用顯微鏡觀察懸浮在水中花粉的運動而發現的。作布朗運動的
粒子 非常微小,直徑約1~10微米, 在周圍液體或氣體分子的碰撞下,產生一種漲落不定的淨
作用力 ,導致微粒的布朗運動。如果布朗粒子相互碰撞的機會很少,可以看成是巨大分子組成的理想氣體,則在
重力場 中達到
熱平衡 後,其數密度按高度的分布應遵循玻耳茲曼分布(
麥克斯韋-玻爾茲曼分布 )。J.B.
佩蘭 的實驗證實了這一點,並由此相當精確地測定了
阿伏伽德羅常量 及一系列與微粒有關的數據。1905年A.
愛因斯坦 根據擴散方程建立了布朗運動的統計理論。布朗運動的發現、實驗研究和理論分析間接地證實了分子的無規則
熱運動 ,對於
氣體動理論 的建立以及確認物質結構的
原子 性具有重要意義,並且推動
統計物理學 特別是漲落理論的發展。由於布朗運動代表一種隨機漲落現象,它的理論對於儀表
測量精度 限制的研究以及高倍放大電訊電路中背景噪聲的研究等有廣泛套用。
這是1826年英國植物學家
布朗 (1773-1858)用顯微鏡觀察懸浮在水中的花粉時發現的。後來把懸浮微粒的這種運動叫做布朗運動。不只是花粉和小炭粒,對於液體中各種不同的懸浮微粒,都可以觀察到布朗運動。布朗運動可在氣體和液體中進行。
特點 無規則
每個液體分子對小顆粒撞擊時給顆粒一定的瞬時衝力,由於分子運動的無規則性,每一瞬間,每個分子撞擊時對小顆粒的衝力大小、方向都不相同,合力大小、方向隨時改變,因而布朗運動是無規則的。
永不停歇
因為液體分子的運動是永不停息的,所以液體分子對固體微粒的撞擊也是永不停息的。
顆粒越小,布朗運動越明顯
顆粒越小,顆粒的表面積越小,同一瞬間,撞擊顆粒的液體分子數越少,據統計規律,少量分子同時作用於小顆粒時,它們的合力是不可能平衡的。而且,同一瞬間撞擊的分子數越少,其合力越不平衡,又顆粒越小,其質量越小,因而顆粒的加速度越大,運動狀態越容易改變,故顆粒越小,布朗運動越明顯。
溫度越高,布朗運動越明顯
溫度越高,液體分子的運動越劇烈,分子撞擊顆粒時對顆粒的撞擊力越大,因而同一瞬間來自各個不同方向的液體分子對顆粒撞擊力越大,小顆粒的運動狀態改變越快,故溫度越高,布朗運動越明顯。
肉眼看不見
做布朗運動的固體顆粒很小,肉眼是看不見的,必須在顯微鏡才能看到。
布朗運動間接反映並證明了分子熱運動。
產生原因 1827年,蘇格蘭植物學家
羅伯特·布朗 發現水中的花粉及其它懸浮的微小顆粒不停地作不規則的
曲線運動 ,稱為布朗運動。人們長期都不知道其中的原理。50年後,J·德耳索提出這些微小顆粒是受到周圍分子的不平衡的碰撞而導致的運動。後來得到愛因斯坦的研究的證明。布朗運動也就成為
分子運動論 和
統計力學 發展的基礎。
懸浮在液體或氣體中的微粒(
線度 ~10
-3 mm)表現出的永不停止的無規則運動,如墨汁稀釋後碳粒在水中的無規則運動,藤黃顆粒在水中的無規則運動……。而且溫度越高,微粒的布朗運動越劇烈。布朗運動代表了一種隨機漲落現象。
布朗運動是大量分子做無規則運動對懸浮的固體微粒各個方向撞擊作用的不均衡性造成的,所以布朗運動是大量液體分子集體行為的結果。
歷史進程 布朗的發現是一個新奇的現象,它的原因是什麼?人們是迷惑不解的。在布朗之後,這一問題一再被提出,為此有許多學者進行過長期的研究。一些早期的研究者簡單地把它歸結為熱或電等外界因素引起的。最早隱約指向合理解釋的是
維納 (1826——1896),1863年他提出布朗運動起源於分子的振動,他還公布了首次對微粒速度與粒度關係的觀察結果。不過他的分子模型還不是現代的模型,他看到的實際上是微粒的位移,並不是振動。
流動根源 在維納之後,S·埃克斯納也測定了微粒的移動速度。他提出布朗運動是由於微觀範圍的流動造成的,他沒有說明這種流動的根源,但他看到在加熱和光照使液體粘度降低時,微粒的運動加劇了。就這樣,維納和S·埃克斯納都把布朗運動歸結為物系自身的性質。這一時期還有康托尼,他試圖在熱力理論的基礎上解釋布朗運動,認為微粒可以看成是巨大分子,它們與液體介質處於
熱平衡 ,它們與液體的相對運動起源於
滲透作用 和它們與周圍液體之間的相互作用。
撞擊微粒 到了70——80年代,一些學者明確地把布朗運動歸結為液體分子撞擊微粒的結果,這些學者有卡蓬內爾、德爾索和梯瑞昂,還有耐格里。植物學家耐格里(1879)從真菌、細菌等通過空氣傳播的現象,認為這些微粒即使在靜止的空氣中也可以不沉。聯繫到物理學中氣體分子以很高速度向各方向運動的結論,他推測在陽光下看到的飛舞的塵埃是氣體分子從各方向撞擊的結果。他說:“這些微小塵埃就象彈性球一樣被擲來擲去,結果如同分子本身一樣能保持長久的懸浮。”不過耐格里又放棄了這一可能達到正確解釋的途徑,他計算了單個氣體分子和塵埃微粒發生
彈性碰撞 時微粒的速度,結果要比實際觀察到的小許多數量級,於是他認為由於氣體分子運動的無規則性,它們共同作用的結果不能使微粒達到觀察速度值,而在液體中則由於介質和微粒的
摩擦阻力 和分子間的
粘附力 ,分子運動的構想不能成為合適的解釋。
解決難題 1874——1880年間,卡蓬內爾、德耳索和梯瑞昂的工作解決了耐格里遇到的難題。這裡的關鍵是他們認為由於分子運動的無規則性和分子速度有一分布,在液體或氣體中的微觀尺度上存在密度和壓力的漲落。這種漲落在巨觀尺度上抵消掉了。但是如果壓方面足夠微小,這種不均勻性就不能抵消,液體中的相應的擾動就能表現出來。因此懸浮在液體中的微粒只要足夠小,就會不停地振盪下去。卡蓬內爾明確地指出唯一影響此效應的因素是微粒的大小,不過他把這種運動主要看成振盪,而德耳索根據
克勞修斯 把分子運動歸結為平動和轉動的觀點,認為微粒的運動是無規則位移,這是德耳索的主要貢獻。
實驗觀察 此後,古伊在1888——1895年期間對布朗運動進行過大量的實驗觀察。古伊對分子行為的描述並不比卡蓬內爾等人高明,他也沒有弄清漲落的見解。不過他的特別之處是他強調的不是對布朗運動的物理解釋,而是把布朗運動作為探究分子運動性質的一個工具。他說:“布朗運動表明,並不是分子的運動,而是從分子運動導出的一些結果能向我們提供直接的和可見的證據,說明對熱本質假設的正確性。按照這樣的觀點,這一現象的研究承擔了對
分子物理學 的重要作用。”古伊的文獻產生過重要的影響,所以後來貝蘭把布朗運動正確解釋的來源歸功於古伊。
研究工作 到了1900年,F·埃克斯納完成了布朗運動前期研究的最後工作。他用了許多
懸濁液 進行了和他的父親S·埃克斯納30年前作過的同類研究。他測定了微粒在1min內的位移,與前人一樣,證實了微粒的速度隨粒度增大而降低,隨溫度升高而增加。他清楚地認識到微粒作為巨大分子加入了液體分子的熱運動,指出從這一觀點出發“就可以得出微粒的
動能 和溫度之間的關係。”他說:“這種可見的運動及其測定值對我們清楚了解液體內部的運動會有進一步的價值”。
研究情況 以上是1900年前對布朗運動研究的基本情況。自然,這些研究與分子運動論的建立是密切相關的。由麥克斯威(
詹姆斯·克拉克·麥克斯韋 )和玻爾茲曼(
路德維希·玻爾茲曼 )在60——70年代建立的
氣體分子運動論 在概念上的一個重大發展是拋棄了對單個分子進行詳細跟蹤的方法,而代之以對大量分子的統計處理,這為弄清布朗運動的根源打下了基礎。與布朗運動的研究有密切關係的還有在60年代由
格雷哈姆 建立的
膠體 科學。所謂膠體是由粒度介於巨觀
粒子 和
微觀 分子之間的微粒形成的
分散體系 ,布朗運動正是膠體粒子在液體介質中表現的運動。
對於布朗運動的研究,1900年是個重要的分界線。至此,布朗運動的適當的物理模型已經顯明,剩下的問題是需要作出定量的理論描述了。
愛因斯坦 1905年,
愛因斯坦 依據分子運動論的原理提出了布朗運動的理論。就在差不多同時,斯莫盧霍夫斯基也作出了同樣的成果。他們的理論圓滿地回答了布朗運動的本質問題。
應該指出,愛因斯坦從事這一工作的歷史背景是那時科學界關於分子真實性的爭論。這種爭論由來已久,從
原子 分子理論產生以來就一直存在。本世紀初,以物理學家和哲學家馬赫和化學家奧斯特瓦爾德為代表的一些人再次提出對原子分子理論的非難,他們從實證論或唯能論的觀點出發,懷疑原子和分子的真實性,使得這一爭論成為科學前沿中的一個中心問題。要回答這一問題,除開哲學上的分歧之外,就科學本身來說,就需要提出更有力的證據,證明原子、分子的真實存在。比如以往測定的
相對原子質量 和
相對分子質量 只是質量的相對比較值,如果它們是真實存在的,就能夠而且也必須測得相對原子質量和相對分子質量的絕對值,這類問題需要人們回答。
由於上述情況,像愛因斯坦在論文中指出的那樣,他的目的是“要找到能證實確實存在有一定大小的
原子 的最有說服力的事實。”他說:“按照熱的分子運動論,由於熱的分子運動,大小可以用顯微鏡看見的物體懸浮在液體中,必定會發生其大小可以用顯微鏡容易觀測到的運動。可能這裡所討論的運動就是所謂‘布朗分子運動’”。他認為只要能實際觀測到這種運動和預期的規律性,“精確測定原子的實際大小就成為可能了”。“反之,要是關於這種運動的預言證明是不正確的,那么就提供了一個有份量的證據來反對
熱分子 運動觀”。
原理推導 愛因斯坦的成果大體上可分兩方面。一是根據
分子熱運動 原理推導:在t時間裡,微粒在某一方向上位移的統計平均值,即
方均根值 ,D是微粒的擴散係數。這一公式是看來毫無規則的布朗運動服從分子熱運動規律的必然結果。
愛因斯坦成果的第二個方面是對於球形微粒,推導出了可以求算阿式中的η是介質粘度,a是微粒半徑,R是
氣體常數 ,NA為
阿伏加德羅常數 。按此公式,只要實際測得準確的擴散係數D或布朗運動均方位移就可得到原子和分子的絕對質量。愛因斯坦曾用前人測定的糖在水中的擴散係數,估算的NA值為3.3×10^23,一年後(1906),又修改為6.56×10^23。
真實性 愛因斯坦的理論成果為證實分子的真實性找到了一種方法,同時也圓滿地闡明了布朗運動的根源及其規律性。下面的工作就是要用充足的實驗來檢驗這一理論的可靠性。愛因斯坦說:“我不想在這裡把可供我使用的那些稀少的實驗資料去同這理論的結果進行比較,而把它讓給實驗方面掌握這一問題的那些人去做”。“但願有一位研究者能夠立即成功地解決這裡所提出的、對熱理論關係重大的這個問題!”愛因斯坦提出的這一任務不久之後就由貝蘭(1870——1942)和
斯維德伯格 分別出色的完成了。這裡還應該提到本世紀初在研究布朗運動方面一個重大的實驗進展是1902年齊格蒙第(1865——1929)發明了
超顯微鏡 ,用它可直接看到和測定膠體粒子的布朗運動,這也就是證實了膠體粒子的真實性,為此,齊格蒙第曾獲1925年諾貝爾化學獎。斯維德伯格測定布朗運動就是用超顯微鏡進行的。
貝蘭實驗 1908到1913年期間,貝蘭進行了驗證愛因斯坦理論和測定阿伏加德羅常數的實驗研究。他的工作包括好幾方面。在初期,他的想法是,既然在液體中進行布朗運動的微粒可以看成是進行熱運動的巨大分子,它們就應該遵循分子運動的規律,因此只要找到微粒的一種可用實驗觀測的性質,這種性質與
氣體定律 在邏輯上是等效的,就可以用來測定
阿伏加德羅常數 。1908年,他想到液體中的懸浮微粒相當於“可見分子的微型大氣”,所以微粒濃度(單位體積中的數目)的高度分布公式應與氣壓方程有相同的形式,只是對
粒子 受到的浮力應加以校正。這一公式是:ln(n/n0)=-mgh(1-ρ/ρ0)/kt。式中k是波爾茲曼常數,自k和NA的關係,公式也可寫成ln(n/n0)=-NA mgh(1-ρ/ρ0)/RT。根據此公式,從實驗測定的粒子濃度的高度分布數據就可以計算k和NA。
為進行這種實驗,先要製得合用的微粒。製備方法是先向樹脂的酒精溶液中加入大量水,則樹脂析出成各種尺寸的小球,然後用
沉降分離 的方法多次分級,就可以得到大小均勻的級份(例如直徑約3/4μm的藤黃球)。用一些精細的方法測定小球的直徑和密度。下一步是測定
懸浮液 中小球的高度分布,是將懸浮液裝在透明和密閉的盤中,用顯微鏡觀察,待
沉降 達到平衡後,測定不同高度上的粒子濃度。可以用快速照相,然後計數。測得高度分布數據,即可計算NA。貝蘭及其同事改變各種實驗條件:材料(藤黃、乳香),粒子質量(從1到50),密度(1.20到1.06),介質(水,濃糖水,甘油)和溫度(-90°到60°),得到的NA值是6.8×10^23。
直接證明 貝蘭的另一種實驗是測量布朗運動,可以說這是對
分子熱運動 理論的更直接證明。根據前述的愛因斯坦對球形粒子導出的公式,只要實驗液,在選定的一段時間內用顯微鏡觀察粒子的
水平投影 ,測得許多位移數值,再進行統計平均。貝蘭改變各種實驗條件,得到的NA值是(5.5-7.2)×10。貝蘭還用過一些其它方法,用各種方法得到的NA值是:
6.5×10 用類似氣體懸浮液分布法,
6.2×10 用類似液體懸浮液分布法,
6.0×10 測定濃懸浮液中的騷動,
6.5×10測定平動布朗運動,
6.5×10 測定轉動布朗運動。
這些結果相當一致,都接近現代公認的數值6.022×10^23。考慮到方法涉及許多物理假設和實驗技術上的困難,可以說這是相當了不起的。以後的許多研究者根據其它原理測定的NA值都肯定了貝蘭結果的正確性。與貝蘭差不多同時,斯維德伯格(1907)用
超顯微鏡 觀測
金溶膠 的布朗運動,在測定阿伏加德羅常數和驗證愛因斯坦理論上也作出了出色的工作。可以說他們是最先稱得
原子質量 的人,所以在1926年,貝蘭和斯維德伯格分別獲得了諾貝爾物理學獎和化學獎。
現代研究 就這樣,布朗運動自發現之後,經過多半個世紀的研究,人們逐漸接近對它的正確認識。到本世紀初,先是愛因斯坦和斯莫盧霍夫斯基的理論,然後是貝蘭和斯維德伯格的實驗使這一重大的
科學問題 得到圓滿地解決,並首次測定了阿伏加德羅常數,這也就是為分子的真實存在提供了一個直觀的、令人信服的證據,這對
基礎科學 和哲學有著巨大的意義。從這以後,科學上關於
原子 和分子真實性的爭論即告終結。正如原先
原子論 的主要反對者奧斯特瓦爾德所說:“布朗運動和動力學假說的一致,已經被貝蘭十分圓滿地證實了,這就使哪怕最挑剔的科學家也得承認這是充滿空間的物質的原子構成的一個實驗證據”。數學家和物理學家彭加勒在1913年總結性地說道:“貝蘭對原子數目的光輝測定完成了原子論的勝利”。“化學家的原子論現在是一個真實存在”。
布朗運動代表了一種隨機漲落現象,它的理論在其他領域也有重要套用。如對測量儀器的精度限度的研究;高倍放大電訊電路中的背景噪聲的研究等
布朗運動與
分子熱運動 不一樣,與溫度和粒子個數有關,溫度越高,布朗運動越劇烈,粒子越少,分子熱運動越劇烈。
分子永不停息地做無規則的運動。布朗運動、
擴散現象 都說明了任何物質的分子,不論在什麼狀態下,都在做永不停息的無規則運動。分子的無規則運動與物質的溫度有關,溫度越高,分子的無規則運動越劇烈。
力學平衡 按經典
熱力學 的觀點,布朗運動嚴格來說屬於
機械運動 ,因此它表現出的是一種
機械能 。這種機械能是自發由內能轉化而來,而與同時,它又在向內能轉化而去,當這兩種轉化的速率相同時,客觀上就達到了一種
動態平衡 ,表現為顆粒做布朗運動。此時兩種能自發地不停地相互轉化,而不引起其它變化。
有人據此對
熱力學第二定律 提出質疑。實際上,布朗運動是一種特殊的機械運動,做布朗運動的顆粒正好處於巨觀與微觀的分界點上,所以布朗運動中機械能同時具有一般意義上的巨觀機械能與微觀
分子動能 的雙重特性,它的能量集中程度介於兩者之間,
無序性 也介於兩者之間。
熱力學第二定律本身只適用於巨觀物體,而布朗運動的問題,實際上反映了經典物理學“巨觀”與“
微觀 ”概念的
模糊性 ,也反映了經典物理學的局限。而這種特殊的運動能否像人們希望的那樣把人類從滅頂於熵的悲劇中拯救出來,只能從
量子物理學 中尋求答案。
相關課題 無規則行走(random walk)
定義:無規則行走就是
隨機遊走 。其概念接近於布朗運動,
是布朗運動的理想數學狀態 。
核心概念:任何無規則行走者所帶的守恆量都各自對應著一個擴散運輸定律。
無規則行走只是布朗運動的理想狀態
無規則行走只是布朗運動的理想狀態二者概念不等同,實際觀測,在納米尺度下,不規則物體布朗運動不滿足
高斯分布 。
在很多系統都存在不同類型的無規則行走,他們都具有相似結構。單個的隨機事件我們不可預測,但隨機大量的群體行為,卻是精確可知的,這就是機率世界的魅力,在偶然中隱含著必然。隨機性造成了低尺度下的差異性,但在高尺度下又表現為共同的特徵的相似性。按照
機率 的觀點“宇宙即是所有隨機事件機率的總和”。
橢球體布朗運動相關研究
雖然無規則行走導致的擴散滿足以上的方程並有普適性,但假如這樣的的“無規則行走”某個方向,並不是完全隨機呢?以前面提到的投硬幣為例子,一個1 分,一個5 分,其中1 分硬幣破損使得正反面機率不相等,並且隨機若干步後,將1 分和5 分硬幣所代表的方向對調;那么二維的無規則行走路徑必然發生改變。當年愛因斯坦的論文是探討球形顆粒的布朗運動,我們知道球形顆粒的旋轉並不影響他的平移,旋轉的非球形例子卻會影響它的平移。實際中,大量布朗運動的顆粒都是非球形的,所以更多的模型不得不考慮隨機轉動問題。其實即使對球形顆粒在
黏性流體 中,也要考慮隨機轉動產生的轉動摩擦係數對擴散的影響。
賓夕法尼亞大學 的網站報導,研究人員用數字視屏顯微鏡觀察水中懸浮
橢球體 的隨機旋轉和移動。球形顆粒擴散分布將隨時間逐漸變寬,為
高斯 型濃度分布;而
橢球 顆粒不滿足高斯分布。隨著布朗運動的深入研究,越來越多的實驗表明布朗運動顆粒的行為與愛因斯坦一個世紀前的假設不同。2005 年10 月的
物理評論快報 ,提到現在實驗室可以跟蹤布朗運動顆粒的
測量精度 達到微秒和納米的尺度。科學家們也發現活細胞的許多基本過程由布朗運動所驅動。試驗結果描述布朗運動的
方程式 偏離標準理論的,實際的布朗運動要比理想化的無規則行走要複雜。
橢球體在水中的布朗運動 右圖是 標準的無規則行走,色彩標記顯示出橢球的耦合方向和位移,並清楚的表明橢球的擴散其長軸比其短軸擴散更快。(此圖來源於賓夕法尼亞大學網站關於布朗運動的研究)
還原論的缺憾
布朗運動是分形的典型例子,理想狀態下的布朗運動是高斯常態分配,當然更多的布朗運動研究細節我們不做探討。任何事物都不是孤立的,都是相互作用、相互聯繫的。用還原論觀點將系統一個個隔離是對事物的理想化,是在一定程度上精確定量描述系統,當然這也是認識事物必經的步驟,但是有缺陷的。
哥德爾不完備定理 ,以及認識主體對客體的反映永遠存在這不完備性。我觀贊同
哥本哈根學派 的主張“自然科學不是自然界本身,而是人和自然界間關係的一部分,因而依賴人”。無論用
還原論 還是
整體論 都是用抽象去闡明物質的特性,這些抽象在任何時候僅僅是近似地、有條件的把握了物質的本質,不是世界的全部。布朗運動研究的歷史,具有典型性,有點像整個科學研究史的縮影。人對事物的認識總是漸進的,不斷深入的,隨著認識深入會發現各種模型都是理想化的條件。這種認識永遠無法走向事物的絕對認識,因為孤立的事物是不存在的,所有的系統都是宇宙整體的一部分。
誤解 值得注意的是,布朗運動指的是花粉迸出的微粒的隨機運動,而不是分子的隨機運動。但是通過布朗運動的現象可以
間接證明 分子的無規則運動。
花粉具備足夠大小,幾乎無法觀測到布朗運動 一般而言,花粉之直徑分布於30~50μm、最小亦有10μm之譜,相較之下,水分子直徑約0.3nm(非球形,故依部位而有些許差異。),概略為花粉之萬分之一,難以令花粉產生不規則振動。因此,花粉事實上幾乎不受布朗運動之影響。在羅伯特·布朗的手稿中,“tiny particles from the pollen grains of flowers”意味著“自花粉粒中迸出之
微粒子 ”,而非指花粉本身。然而在翻譯為諸國語言時,時常受到誤解,以為是“水中的花粉受到水分子撞擊而呈現不規則運動”。積非成是之下,在大眾一般觀念中,此誤會已然根深蒂固。
花粉具備足夠大小,幾乎無法觀測到布朗運動。
在日本,以鶴田憲次‘物理學叢話’為濫觴,岩波書店‘岩波理科辭典’[2]、花輪重雄‘物理學読本’、湯川秀樹‘素粒子’、坂田昌二‘物理學原論(上)’、平凡社‘理科辭典’、福岡伸一著‘生物與無生物之間’,甚至日本的理科課本等等,皆呈現錯誤之敘述。
直到1973年橫浜市立大學名譽教授植物學者岩波洋造在著書‘植物之SEX‐不為人知的性之世界’中,點出此誤謬之前,鮮少有人注意。國立教育研究所物理研究室長板倉聖宣在參與製作岩波電影‘回動粒子’(1970年)時,實際攝影漂浮在水中之花粉,卻發現花粉完全沒有布朗運動。遂於1975年3月,以“外行人與專家之間”為題,解說有關布朗運動之誤會。
機率論 {B(t)}布朗運動(brownian motion)也稱為
維納過程 ,是一個隨機過程,如果滿足以下性質:
1. 獨立的增量(independence of increments)
對於任意的t>s, B(t)-B(s)獨立於之前的過程B(u):0<=u<=s.
2. 正態的增量(normal increments)
B(t)-B(s)滿足均值為0方差為t-s的
常態分配 。即,B(t)-B(s)~ N(0,t-s)。
3. 連續的路徑(continuity of paths)
B(t), t>=0是關於t的
連續函式 。固定一條路徑, B(t)->B(s) 滿足依機率收斂。
金融數學 將布朗運動與股票價格行為聯繫在一起,進而建立起維納過程的數學模型是本世紀的一項具有重要意義的金融創新,在現代金融數學中占有重要地位。迄今,普遍的觀點仍認為,股票市場是隨機波動的,隨機波動是股票市場最根本的特性,是股票市場的常態。
布朗運動假設是現代資本市場理論的核心假設。現代資本市場理論認為證券期貨價格具有隨機性特徵。這裡的所謂隨機性,是指數據的無記憶性,即過去數據不構成對未來數據的預測基礎。同時不會出現驚人相似的反覆。
隨機現象 的數學定義是:在個別試驗中其結果呈現出不確定性;在大量重複試驗中其結果又具有
統計規律性 的現象。描述股價行為模型之一的布朗運動之維納過程是馬爾科夫隨機過程的一種特殊形式;而馬爾科夫過程是一種特殊類型的隨機過程。隨機過程是建立在
機率 空間上的
機率模型 ,被認為是機率論的動力學,即它的研究對象是隨時間演變的
隨機現象 。所以隨機行為是一種具有
統計規律性 的行為。股價行為模型通常用著名的維納過程來表達。假定股票價格遵循一般化的維納過程是很具誘惑力的,也就是說,它具有不變的期望漂移率和方差率。維納過程說明只有變數的當前值與未來的預測有關,變數過去的歷史和變數從過去到現在的演變方式則與未來的預測不相關。股價的馬爾科夫性質與弱型市場有效性(the weak form of market efficiency)相一致,也就是說,一種股票的現價已經包含了所有信息,當然包括了所有過去的價格記錄。但是當人們開始採用分形理論研究金融市場時,發現它的運行並不遵循布朗運動,而是服從更為一般的幾何布朗運動(geometric browmrian motion)。
一維brownian motion 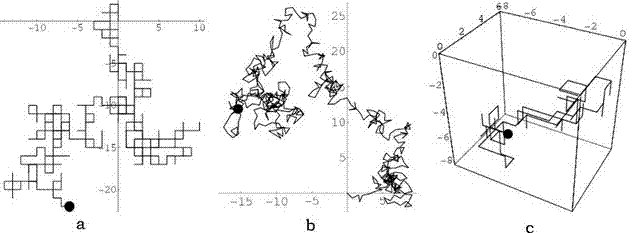
 橢球體在水中的布朗運動
橢球體在水中的布朗運動 花粉具備足夠大小,幾乎無法觀測到布朗運動
花粉具備足夠大小,幾乎無法觀測到布朗運動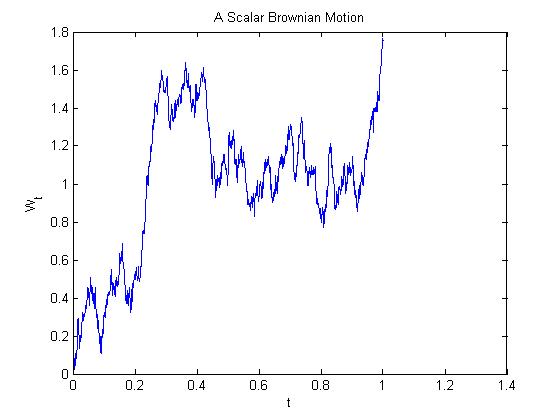 一維brownian motion
一維brownian motion
