拐點,又稱反曲點,在數學上指改變曲線向上或向下方向的點,直觀地說拐點是使切線穿越曲線的點(即曲線的凹凸分界點)。若該曲線圖形的函式在拐點有二階導數,則二階導數在拐點處異號(由正變負或由負變正)或不存在。
基本介紹
- 中文名:拐點
- 外文名:inflection point
- 拼音:guǎi diǎn
- 別稱:反曲點
- 適用範圍:數理科學
定義







存在條件
必要條件



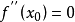
第一充分條件


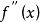



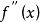


第二充分條件

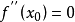
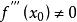

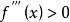
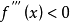
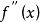
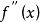
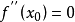


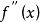

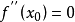
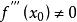


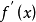
拐點的求法






拐點,又稱反曲點,在數學上指改變曲線向上或向下方向的點,直觀地說拐點是使切線穿越曲線的點(即曲線的凹凸分界點)。若該曲線圖形的函式在拐點有二階導數,則二階導數在拐點處異號(由正變負或由負變正)或不存在。










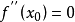


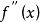



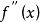



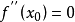
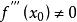

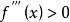
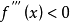
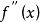
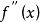
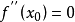


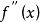

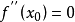
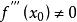


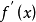






拐點,又稱反曲點,在數學上指改變曲線向上或向下方向的點,直觀地說拐點是使切線穿越曲線的點(即曲線的凹凸分界點)。若該曲線圖形的函式在拐點有二階導數,則二階...
在生活中借指事物的發展趨勢開始改變的地方(例如:經濟運行出現回升拐點)。 在生活中,拐點多用來說明某種情形持續上升一段時間後開始下降或回落。在數學上這句話是...
拐點,傳媒用語。...... 拐點,傳媒用語。所謂“拐點”,原是高等數學中的一個概念,套用到傳媒領域,是指中國媒介改革還存在很大的增量空間。但是,如果按照現行的發展...
拐點分解()。不是通過成核—生長機理而是。在此種方式出溶的早期階段中,在固溶體內並不存在有明顯的兩相界面,且過飽和的組分(例如鉀長石中的Na)在固溶體內的...
《拐點法則》一書作者是韓鐵林,由浙江工商大學出版社出版發行。...... 建立起全局性的思考能力和框架性的思維結構;能夠以拐點法則為線索,看透企業的成長本質,找到企...
C理論是由九指理論研究室發現建立。它是一種拐點理論,其哲學思想是研究一切種類市場價格博弈理論的基礎。...
學科:水文地質學 詞目:拐點法 英文:inflexion-point method 釋文:在有越流補給時,利用抽水試驗資料求含水層參數的一種圖解法。其方法是,當有越流補給時,單井非...
並且,C理論雖然能同步判斷拐點的出現,但卻不能單獨預計未來拐點的時空位置,必須借照其它理論才行。目錄 1 定義由來 2 理論 ▪ 理論內涵 ▪ 基本定理 ...
拐點坐標是劃分礦區區塊的時候用的,比如地質圖上一個正方形區塊,它的四個角的地理坐標就叫區塊的拐點坐標。...
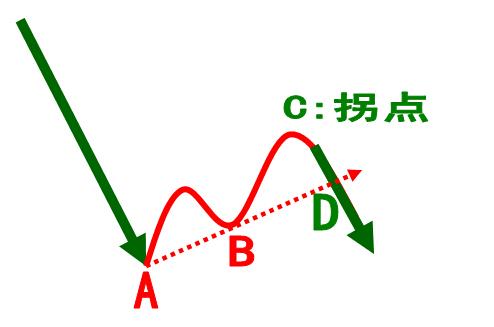
所謂拐點,是指事物或一個行業在其發展過程中在某一區域或某一階段出現並持續一段時間的轉折性發展趨勢變化。...
拐點是事物發展過程中運行趨勢或運行速率的變化,而拐點鏡頭是指在影視作品中出現的一個十分優秀的技巧——人物或物體從以某個參照物為水平面以下逐漸出現並走出水平...
影片《拐點》是由河南省戰旗文化傳播有限公司出品,北京溢彩影視文化傳媒有限公司獨家發行。周洪慶擔任本片總製片人兼監製、編劇,雷丹導演,國家一級演員崔文化領銜主演...
庫茲涅茨拐點是指在經濟發展的初期,環境質量可能隨著經濟成長而不斷下降和惡化,但到一定拐點時,環境質量又有可能隨經濟的進一步發展而逐步改善。...
及時在股票趨勢出現拐點向上的時候立刻介入,從而把握最低的追漲風險;及時在股票趨勢出現拐點向下的時候立刻拋出,從而把握最最高盈利效益。...
人口拐點即在坐標上改變曲線向上或向下方向的點。一般理解意義上,可以認為人口紅利拐點指一個社會人口結構中,勞動人口增長率低於非勞動人口(特別是退休勞動人口)增長...
時間拐點內容簡介 編輯 韓庚,一個從海歸精英淪落為街頭乞丐,卻因為得到一部手機而再次輝煌。他歷經人間滄桑,享盡世間繁華。然而這一切都是以老年孤獨鰥居為代價的,...
“主序拐點”是天文學專有名詞。來自中國天文學名詞審定委員會審定發布的天文學專有名詞中文譯名,詞條譯名和中英文解釋數據著作權由天文學名詞委所有。...
《大拐點》是2012年5月31日中信出版社出版的圖書,作者是袁劍...... 本書想要提醒人們,中國可能已極其接近一個大型的經濟拐點。這個拐點是由全球市場體系的裂變與中...
《暴利在拐點》是2011年7月1日機械工業出版社出版的圖書,作者是王繼洲。...... 為了幫助讀者在實戰中發現拐點、利用拐點獲得利潤,《暴利在拐點》分別從政策、事件、...
本書以全球化競爭視野和大量一手案例為基礎,詳盡分析了中國企業突破拐點的任務與方法,對傳統的戰略管理管理理論、組織變革理論、企業家精神均有創新詮釋和突破性貢獻...
人口紅利拐點目前沒有明確的科學定義。一般理解意義上,可以認為人口紅利拐點指一個社會人口結構中,勞動人口增長率低於非勞動人口(特別是退休勞動人口)增長率的時候...
中文名稱 拐點年齡 英文名稱 age of inflecting point;age at inflection point 定義 體重絕對生長速度達到最大時的年齡。 套用學科 水產學(一級學科),漁業...
