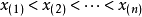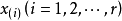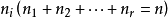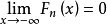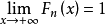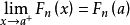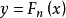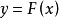樣本分布函式(sample distribution function)亦稱經驗分布函式，統計學中的基本概念之一。樣本分布函式Fn(x)具有分布函式的性質，我們可以將其看成是以等機率1/n 取值X1，X2，…，Xn的離散型隨機變數的分布函式。且該函式的圖形呈跳躍式一條台階形折線，如觀測值不重複，則每一跳躍為1/n ，如有重複，則按1/n的倍數跳躍上升。
基本介紹
- 中文名：樣本分布函式
- 外文名：sample distribution function
- 別稱：經驗分布函式
- 學科：統計學
- 從屬：分布函式
- 套用：機率論圖數理統計，數學
定義,樣本分布函式,圖象意義,性質,推論,舉例,例1,例2,
定義
樣本分布函式
我們知道，若總體是隨機變數X，則X的分布就是總體的分布(也叫理論分布)，X的分布函式便是總體的分布函式。要了解總體的情況，就要了解隨機變數x的分布或它的某些數字特徵。樣本是總體的代表和反映，簡單隨機樣本應該能很好地反映總體的情況。那末，如何由樣本來推斷總體的分布呢?一般做法是作出樣本分布函式用以觀察理論分布的概貌。為此我們給出樣本分布函式的定義。
設(X1，X2，…，Xn)是來自總體X的一個簡單隨機樣本，將其一個觀測值(x1，x2，…xn，)的分量按從小到大的順序排列成
其中
出現的頻數為
，記
稱F(X)為總體X的樣本分布函式或經驗分布函式。
圖象意義
樣本分布函式的圖像也是類似於離散型隨機變數分布函式的圖像，是一條跳躍式上升的階梯形曲線，在每個間斷點x(k)處跳躍。若樣本觀測值的各分量x1，x2，…，xn不重複，則每一躍度為
；若某一分量重複m次，則在該分量處躍度為
。
性質
由此定義容易看出，Fn(x)滿足下列性質：
(1)(單調有界性)樣本分布函式是單調增加的有界函式，且0≤Fn(x)≤1；
(2)(規範性)
，
；
(3)(右連續性)對於任意的實數a，
；
(4)Fn(x)為非減函式；
由此可見，樣本分布函式Fn(x)具有分布函式的性質，我們可以將其看成是以等機率 取值X1，X2，…，Xn的離散型隨機變數的分布函式。
此外，對於任何實數x，Fn*(x)的值等於樣本的n個觀測值中不超過x的個數除以樣本容量n。它正是n次獨立觀測中，事件{X≤x}出現的頻率。由機率與頻率的關係可知，當n充分大時，Fn*(x)可以作為未知分布函式F(x)的一個近似。因此樣本分布函式Fn*(x)可以作為總體分布函式的近似，n越大，近似程度越好.這正是我們用樣本觀測值來估計和推斷總體的一個重要依據。
推論
根據貝努力大數定理，只要n足夠大，Fn(x)依機率收斂於總體分布函式F(x)。事實上還可以有更進一步的結論，這就是格利文科(w．Glivenko)定理
當n足夠大時，Cn的圖形在用不等式
所定的帶狀區域內。
這些結論與下列直觀事實相吻合。在某種燈泡的壽命總體中，隨機地抽取一容量為20的樣本及一容量為120的樣本，其樣本分布函式F20(x)及F120(x)的圖形都是台階形折線。可以看出，對不同容量的樣本，其樣本分布函式也不相同，但都是總體分布函式F(x)的縮影。由此可見，樣本分布函式Fn(x)是總體分布函式F(x)的一個良好近似。
格利文科定理說明了，當n充分大時，格里文科定理深刻地描述了總體X的樣本分布函式Fn(x)近似於總體X的分布函式F(x)。因此對於較大的樣本，樣本分布函式Fn(x)可以作為總體分布函式F(x)的一個很好的近似．這是數理統計學中一切統計推斷都用樣本來估計和推斷總體的理論依據。
舉例
例1
從一批標準重量為5009的罐頭中，隨機抽取8聽，測得誤差如下(單位；g)：8，一4，6，一7，一2，1，0，1，求經驗分布函式，並作出圖形。
解：將樣本值按大小順序排列為：一7<一4<一2<0<1=1<6<8
則其樣本分布函式為：
圖形如下：
例2
設商場100天銷售電視機的情況經統計如下：
求樣分布本函式Fn(x)
解：由樣本分布函式的定義有：
即樣本函式如下：
其圖形如下：
