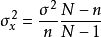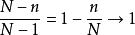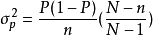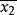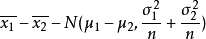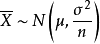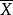抽樣分布也稱統計量分布、隨機變數函式分布，是指樣本估計量的分布。樣本估計量是樣本的一個函式，在統計學中稱作統計量，因此抽樣分布也是指統計量的分布。以樣本平均數為例，它是總體平均數的一個估計量，如果按照相同的樣本容量，相同的抽樣方式，反覆地抽取樣本，每次可以計算一個平均數，所有可能樣本的平均數所形成的分布，就是樣本平均數的抽樣分布。
基本介紹
- 中文名：抽樣分布
- 外文名：Sampling Distribution
- 學科：統計學
- 目的：統計量的分布
- 特點：抽樣分布是統計推斷的理論基礎
- 又名：隨機變數函式分布
類型,單一樣本統計量,兩個樣本統計量,定理,正態總體的抽樣分布,其他分布,
類型
單一樣本統計量
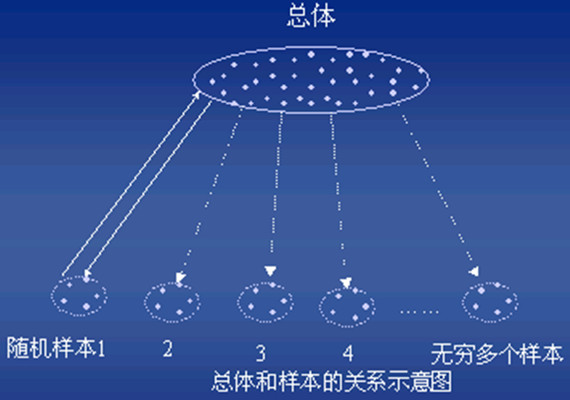
當我們要對某一總體的參數進行估計時，就要研究來自該總體的所有可能的樣本統計量的分布問題，比如樣本均值的分布、樣本比例的分布，從而概括有關統計量抽樣分布的一般規律。
(一)樣本均值的抽樣分布
1．樣本均值抽樣分布的形成
樣本均值的抽樣分布即所有樣本均值的可能取值形成的機率分布。例如，某高校大一年級參加英語四級考試的人數為6000人，為了研究這6000人的平均考分，欲從中隨機抽取500人組成樣本進行觀察。若逐一抽取全部可能樣本，並計算出每個樣本的平均考分，將會得出很多不完全相同的樣本均值，全部可能的樣本均值有一個相應的機率分布，即為樣本均值的抽樣分布。
我們知道，從總體的N個單位中抽取一個容量為n的隨機樣本，在重複抽樣條件下，共有
個可能的樣本；在不重複抽樣條件下，共有
個可能的樣本。因此，樣本均值是一個隨機變數。
2．樣本均值抽樣分布的特徵
從抽樣分布的角度看，我們所關心的分布的特徵主要是數學期望和方差。這兩個特徵一方面與總體分布的均值和方差有關，另一方面也與抽樣的方法是重複抽樣還是不重複抽樣有關。樣本均值的方差則與抽樣方法有關。在重複抽樣條件下，樣本均值的方差為總體方差的1/n，即：
公式一：
在不重複抽樣條件下，樣本均值的方差為：
公式二：
從公式一和公式二可以看出兩者僅相差係數
，該係數通常被稱為有限總體修正係數。在實際套用中，這一係數常常被忽略不計，主要是因為：對於無限總體進行不重複抽樣時，由於N未知，此時樣本均值的標準差仍可按公式一計算，即可按重複抽樣處理；對於有限總體，當N很大而抽樣比例n/N很小時，其修正係數
，通常在樣本容量n小於總體容量N的5%時，有限總體修正係數就可以忽略不計。因此，公式一是計算樣本均值方差的常用公式。
3．樣本均值抽樣分布的形式
樣本均值抽樣分布的形式與原有總體的分布和樣本容量n的大小有關。如果原有總體是常態分配，那么，無論樣本容量的大小，樣本均值的抽樣分布都服從常態分配。如果原有總體的分布是非常態分配，就要看樣本容量的大小。隨著樣本容量n的增大(通常要求n≥30)，不論原來的總體是否服從常態分配，樣本均值的抽樣分布都將趨於常態分配，即統計上著名的中心極限定理。雖然總體成績的分布形態未知，但σ已知，且n=150為大樣本，依據中心極限定理可知：樣本均值的抽樣分布近似服從常態分配。
(二)樣本比例的抽樣分布
樣本比例即指樣本中具有某種特徵的單位所占的比例。樣本比例的抽樣分布就是所有樣本比例的可能取值形成的機率分布。例如，某高校大一年級學生參加英語四級考試的人數有6000人，為了估計這6000人中男生所占的比例，從中抽取500人組成樣本進行觀察，若逐一抽取全部可能樣本，並計算出每個樣本的男生比例，則全部可能的樣本比例的機率分布，即為樣本比例的抽樣分布。可見，樣本比例也是一個隨機變數。
1．樣本比例抽樣分布的特徵
在大樣本情況下，樣本比例的抽樣分布特徵可概括如下：
無論是重複抽樣還是不重複抽樣，樣本比例p的數學期望總是等於總體比例P，即：
公式一：E(p)=P
而樣本比例p的方差，在重複抽樣條件下為：
公式二：
在不重複抽樣條件下為：
2．樣本比例抽樣分布的形式
樣本比例的分布屬於二項分布問題，當樣本容量n足夠大時，即當nP與n(1一P)都不小於5時，樣本比例的抽樣分布近似為常態分配。
兩個樣本統計量
如果要對兩個總體有關參數的差異進行估計，就要研究來自這兩個總體的所有可能樣本相應統計量差異的抽樣分布。
若從總體X1和總體X2 中分別獨立地抽取容量為n1和n2的樣本，則由兩個樣本均值之差
的所有可能取值形成的機率分布稱為兩個樣本均值差異的抽樣分布。
設總體X1和總體X2的均值分別為μ1和μ2，標準差分別為σ1和σ2，則兩個樣本均值之差
的抽樣分布可概括為以下兩種情況：
(1)若總體X1-
，總體X2-
，則
(2)若兩個總體都是非正態總體，當兩個樣本容量n1和n2都足夠大時，依據中心極限定理，
和
分別近似服從常態分配，則
定理
(1)從總體中隨機抽取容量為n的一切可能個樣本的平均數之平均數，等於總體的平均數，即
，(E為平均的符號,
為樣本的平均數，μ為總體的平均數)。
(2)從正態總體中，隨機抽取的容量為n的一切可能樣本平均數的分布也呈常態分配。
(3)雖然總體不是常態分配，如果樣本容量較大，反映總體μ和σ的樣本平均數的抽樣分布，也接近於常態分配。
正態總體的抽樣分布
1°
；
2°
；
3°
與S2獨立。
其他分布
統計中用隨機變數X的取值範圍及其取值機率的序列來描述這個隨機變數，稱之為隨機變數X的機率分布。如果我們知道隨機變數X的取值範圍及其取值機率的序列，就可以用某種函式來表述X取值小於某個值的機率，即為分布函式：F(X)=P(X≤z)。
例如，一個由N家工業企業組成的總體，X為銷售收入。將總體所有企業的銷售收入按大小順序排隊，累計出總體中銷售收入小於某值x的企業數量並除以總體企業總數N，就可得到總體中銷售收入小於x的企業的頻率，也即抽取一個銷售收入小於x的企業的機率。此頻率或機率隨著x值不同而變化形成一個序列，形成了銷售收入X的機率分布。
總體分布是在總體中X的取值範圍及其機率。
樣本分布是在樣本中X的取值範圍及其機率。上例中，如果抽取n個企業作為樣本，我們同樣可以用這n個銷售收入的取值範圍及其機率描述其分布，也即樣本分布。樣本分布也稱為經驗分布，隨著樣本容量n的逐漸增大，樣本分布逐漸接近總體分布。
抽樣分布是指樣本統計量的機率分布。採用同樣的抽樣方法和同等的樣本量，從同一個總體中可以抽取出許許多多不同的樣本，每個樣本計算出的樣本統計量的值也是不同的。樣本統計量也是隨機變數，抽樣分布則是樣本統計量的取值範圍及其機率。
研究機率分布對於抽樣調查是十分重要的，因為只有知道機率分布，才能夠利用抽樣技術推斷抽樣誤差。現實中，總體的分布狀況通常是未知的，但我們也無需知道總體分布，而只需知道抽樣分布。
