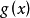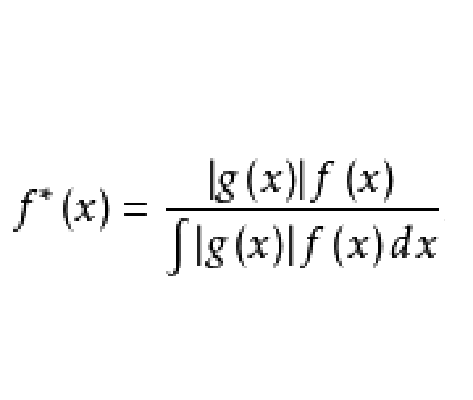重要抽樣法(importance sampling method)是最有效的蒙特卡羅技巧之一,其主要思想是,它不從給定的機率分布函式中進行抽樣,而是對所給定的機率分布進行修改,使得對模擬結果有重要貢獻的部分多出現,從而達到提高效率,減少模擬的時間,以及縮減方差的目的。
基本介紹
- 中文名:重要抽樣法
- 外文名:importance sampling method
- 別名:偏倚抽樣法
- 所屬學科:數學(統計學)
- 相關概念:蒙特卡羅法,方差,分布函式等
基本介紹,相關分析,重要抽樣法的局限性,
基本介紹
考慮如下積分的蒙特卡羅計算問題




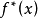


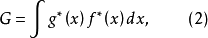





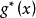




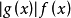
相關分析
重要抽樣法對應於數學上的變數代換方法。即


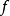



如果 選擇恰當,以使它在積分域內的函式形狀與
選擇恰當,以使它在積分域內的函式形狀與 接近,則該方差可以變得很小。因
接近,則該方差可以變得很小。因


而函式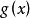 的選擇十分關鍵,它應滿足如下條件:
的選擇十分關鍵,它應滿足如下條件:
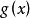
(1)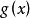 應當是個分布密度函式。
應當是個分布密度函式。
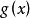
(2)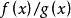 不應起伏太大,使之儘量在積分域內近似等於常數,以保證方差
不應起伏太大,使之儘量在積分域內近似等於常數,以保證方差 比
比 小。
小。
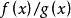


(3)密度函式 對應的分布函式
對應的分布函式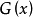 ,能較方便地解析求出。
,能較方便地解析求出。

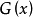
(4)能方便地產生在積分域內,滿足分布函式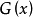 分布的隨機點。
分布的隨機點。
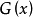
如能按上述條件找到函式 ,就可以依下列步驟求積分:
,就可以依下列步驟求積分:

(1)根據密度函式 產生隨機點
產生隨機點 ,例如採用反函式法。
,例如採用反函式法。


(2)求出各抽樣點 的函式值
的函式值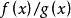 ,並將所有點的該函式值疊加起來除以抽樣點數
,並將所有點的該函式值疊加起來除以抽樣點數 就得到積分結果。
就得到積分結果。

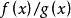

也可採用 作為分布密度函式,利用舍選法以捨去或接受各隨機點
作為分布密度函式,利用舍選法以捨去或接受各隨機點 的值。用此方法時,應當至少可以事先以經驗判斷出
的值。用此方法時,應當至少可以事先以經驗判斷出 的最大值。當然最好能從
的最大值。當然最好能從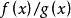 中,推導出
中,推導出 ,但在很多時候這是比較困難的。
,但在很多時候這是比較困難的。



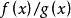

以上的討論可很容易地推廣到更高維的積分計算中,但要注意如下兩方面的問題:第一,在產生隨機向量的某個分量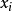 時,沒有必要用舍選法,在產生了隨機向量
時,沒有必要用舍選法,在產生了隨機向量 的所有分量後,再用舍選法往往更快,效率更高。第二,在計算
的所有分量後,再用舍選法往往更快,效率更高。第二,在計算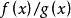 值之前,作隨機變數
值之前,作隨機變數 到
到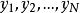 的變換有時是很有用的,這時需將雅可比行列
的變換有時是很有用的,這時需將雅可比行列 包括在權重因子內。
包括在權重因子內。
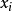

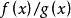

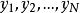

重要抽樣法的局限性
重要抽樣法無疑是蒙特卡羅計算中最基本和常用的技巧之一,它無論在提高計算速度和增加數值結果的穩定性方面都有很大的潛力,但是它仍有一些局限性,譬如:
(1) 尋找分布函式 ,並能解析求出其對應的分布函式
,並能解析求出其對應的分布函式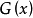 的情況並不多。當然也可用數值計算方法求出
的情況並不多。當然也可用數值計算方法求出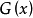 ,但通常這樣處理不靈活速度也慢,並且也不精確。
,但通常這樣處理不靈活速度也慢,並且也不精確。

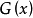
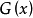
(2) 當選擇 在某點為零或很快趨於零時(如高斯分布),這時是很危險的,其方差
在某點為零或很快趨於零時(如高斯分布),這時是很危險的,其方差 可能趨於無窮大。即使是在某點
可能趨於無窮大。即使是在某點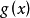 不為零,但卻很小時,方差
不為零,但卻很小時,方差 也可能很大,但是通常採用的從樣本點估計方差的方法卻可能不能檢查出來,這會使得結果不穩定。
也可能很大,但是通常採用的從樣本點估計方差的方法卻可能不能檢查出來,這會使得結果不穩定。