基本介紹
- 中文名:重要性採樣
- 外文名:importance sampling
簡介
目標
原理
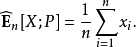
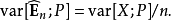

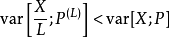
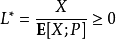
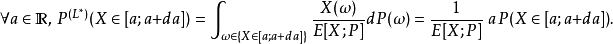
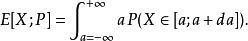

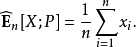
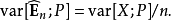

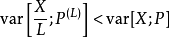
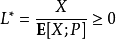
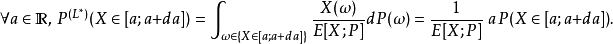
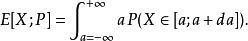
重要性採樣(英語:importance sampling)是統計學中估計某一分布性質時使用的一種方法。該方法從與原分布不同的另一個分布中採樣,而對原先分布的性質進行估計。重要...
重要性重採樣 (Sampling Importance Resampling),是粒子濾波中的一個採樣方法。 傳統分粒子濾波器套用順序重要性採樣(sequential importance sampling, SIS),會引起粒子...
採樣電阻簡介 編輯 電流採樣和對電壓採樣。對電流採樣則串聯一個阻值較小的電阻,對電壓採樣則並聯一個阻值較大的電阻。採樣電阻作用 編輯 ...
12.2 似然加權與重要性採樣 ... 48012.2.1 似然加權:直覺 . 48012.2.2 重要性採樣 . 48212.2.3 貝葉斯網的重要性採樣 . 486...
本書從實用性和先進性出發,較全面地介紹了紅外目標探測的基本理論與相關算法。...15.1.2 序列重要性採樣 30615.1.3 粒子濾波的整體流程 30915.2 粒子觀測...
其核心思想是通過從後驗機率中抽取的隨機狀態粒子來表達其分布,是一種順序重要性採樣法(Sequential Importance Sampling)。簡單來說,粒子濾波法是指通過尋找一組在...
19.2重要性採樣 19.3採樣算法 19.3.1逆變換採樣 19.3.2拒絕採樣 19.3.3馬爾可夫鏈蒙特卡羅方法 第20章貝葉斯混合模型 20.1高斯混合模型 20.1.1貝葉斯公式...
3.2.5 小結3.3 貝葉斯採樣方案3.3.1 引言3.3.2 梗概3.3.3 貝葉斯分類器的採樣類型3.3.4 拒絕採樣3.3.5 均勻比3.3.6 重要性採樣...
4.3.2 蒙特卡洛採樣4.3.3 貝葉斯重要性採樣4.3.4 序列化重要性採樣4.3.5 粒子濾波(Particle Filte)一般算法描述4.3.6 粒子數目N的選取4.4 多視角目標跟蹤...
6 3 1蒙特卡洛採樣原理6 3 2貝葉斯重要性採樣6 3 3序列重要性採樣濾波器6 3 4Bootstrap/SIR濾波器6 3 5權值計算方法6 4粒子濾波經典採樣算法...
2.4 重要性採樣 292.5 資訊理論基礎 332.6 KL 散度 352.7 凸函式及其性質 392.8 機器學習的基本概念 412.9 機器學習的目標函式 432.10 總結 45...
