所謂粒子濾波就是指：通過尋找一組在狀態空間中傳播的隨機樣本來近似的表示機率密度函式，用樣本均值代替積分運算，進而獲得系統狀態的最小方差估計的過程，這些樣本被形象的稱為“粒子”，故而叫粒子濾波。
基本介紹
- 中文名：粒子濾波
- 外文名：Particle Filter
- 簡稱：PF
- 缺點：需要用大量的樣本數量
粒子濾波介紹,進展與展望,粒子濾波發展,
粒子濾波介紹
與卡爾曼濾波（Kalman Filter）相比較
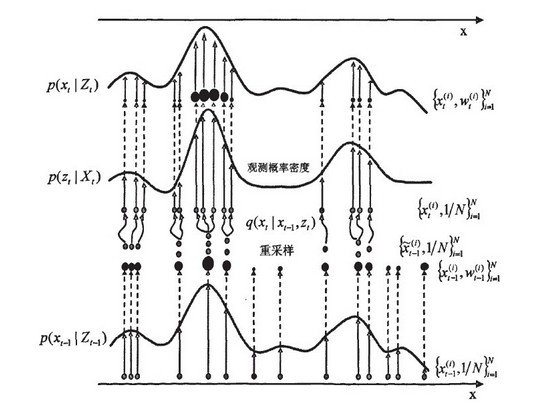
粒子濾波(PF: Particle Filter)的思想基於蒙特卡洛方法(Monte Carlo methods)，它是利用粒子集來表示機率，可以用在任何形式的狀態空間模型上。其核心思想是通過從後驗機率中抽取的隨機狀態粒子來表達其分布，是一種順序重要性採樣法(Sequential Importance Sampling)。簡單來說，粒子濾波法是指通過尋找一組在狀態空間傳播的隨機樣本對機率密度函式進行近似，以樣本均值代替積分運算，從而獲得狀態最小方差分布的過程。這裡的樣本即指粒子,當樣本數量N→∝時可以逼近任何形式的機率密度分布。
儘管算法中的機率分布只是真實分布的一種近似，但由於非參數化的特點，它擺脫了解決非線性濾波問題時隨機量必須滿足高斯分布的制約，能表達比高斯模型更廣泛的分布，也對變數參數的非線性特性有更強的建模能力。因此，粒子濾波能夠比較精確地表達基於觀測量和控制量的後驗機率分布，可以用於解決SLAM問題。
粒子濾波的套用
粒子濾波技術在非線性、非高斯系統表現出來的優越性，決定了它的套用範圍非常廣泛。另外，粒子濾波器的多模態處理能力，也是它套用廣泛的原因之一。國際上，粒子濾波已被套用於各個領域。在經濟學領域，它被套用在經濟數據預測；在軍事領域已經被套用於雷達跟蹤空中飛行物，空對空、空對地的被動式跟蹤；在交通管制領域它被套用在對車或人視頻監控；它還用於機器人的全局定位。
粒子濾波的缺點
雖然粒子濾波算法可以作為解決SLAM問題的有效手段，但是該算法仍然存在著一些問題。其中最主要的問題是需要用大量的樣本數量才能很好地近似系統的後驗機率密度。機器人面臨的環境越複雜，描述後驗機率分布所需要的樣本數量就越多，算法的複雜度就越高。因此，能夠有效地減少樣本數量的自適應採樣策略是該算法的重點。另外，重採樣階段會造成樣本有效性和多樣性的損失，導致樣本貧化現象。如何保持粒子的有效性和多樣性，克服樣本貧化，也是該算法研究重點。
進展與展望
粒子濾波器的套用領域
在現代目標跟蹤領域，由於實際問題的複雜性，所面對的更多的是非線性非高斯問題，Hue等把PF推廣到多目標跟蹤和數據關聯 ，Gordon等對雜波中的目標跟蹤問題提出混合粒子濾波器弼 ，Mcginnity等提出機動目標跟蹤的多模型粒子濾波器 ，Doucet等對跳躍Markov系統狀態估計提出了更有效的PF算法 j，Guo把PF用於感測器網路下的協同跟蹤 J，Freitas等用PF訓練神經網路 ，Srivastava等把PF用於自動目標識別 ，Fox等把PF用於移動機器人定位 ，Ward等提出語音源定位的PF算法，Orton等對來自多個感測器的無序量測提出基於PF的多目標跟蹤和信息融合方法 ，Penny等使用PF實現多感測器資源最優管理和部署 ，Hernandez等結合PF、數據融合和最佳化算法實現多感測器資源管理 ．研究表明PF是解決此類非線性問題的有力工具之一．PF在計算機視覺、可視化跟蹤領域被稱為凝聚算法(CONDENsATION)，該領域是PF的一個非常活躍的套用領域，Bruno提出圖像序列中目標跟蹤的PF算法 ，Maskell等提出基於圖像感測器多目標跟蹤的PF算法_4 ．在聽覺視覺聯合目標定位和跟蹤方面，Vermaak等利用PF提出聲音和視覺融合的集成跟蹤 ，Zotkin等使用PF將來自多個攝像機和麥克風組的視覺聽覺信息融合跟蹤移動目標。
在粒子濾波算法下一些傳統的難點問題如目標檢測、遮擋、交叉、失跟等得到更好的結果．在無線通訊中PF被廣泛用於信道盲均衡、盲檢測、多用戶檢測等方面．其它的套用領域還有機器人視覺跟蹤 、導航 、圖象處理 、生物信息 引、故障診斷和過程控制 、金融數據處理 等．研究表明在有關非高斯非線性系統的數據處理和分析領域PF都具有潛在的套用價值．值得一提的是國內學者在PF的研究上也取得許多成果，莫等利用PF算法提出一種混合系統狀態監測與診斷的新方法 ，Chen等利用PF預測非線性系統狀態分布，獲得故障預測機率 ，Li等提出基於PF的可視化輪廓跟蹤方法 J，Shan等提出基於PF的手形跟蹤識別方法 ，Hu等提出閃爍噪聲下的PF跟蹤算法 等，這些工作推動PF在國內的研究．
粒子方法的新發展
粒子濾波器採用一組隨機粒子逼近狀態的後驗機率分布，有可能用粒子逼近平滑分布，由於重採樣使得粒子喪失多樣性，直接由濾波分布邊緣化得到的平滑分布效果很差，Doucet等套用MCMC方法增加樣本多樣性用於固定延遲平滑取得好的效果，Fong等把RBPF推廣到粒子平滑器，並用於語音信號處理 1．
在PF的性能最佳化方面，目前大多最佳化某個局部的性能指標，如重要性權的方差等，Doucet等使用隨機逼近對PF關於某個全局性能指標進行線上最佳化 ，Chan等人進一步利用SPSA隨機最佳化方法最佳化PF ，避免1r梯度的計算．為了減少計算量使得PF能用於實時數據處理，Foxt提出了粒子個數可變的自適應粒子濾波器 ，Kwok等把粒子劃分為小的集合，每個小樣本集可以進行實時處理，採用加權和的方法逼近狀態後驗分布 ，Brun等提出PF的並行結構算法以獲得線上實時套用 ．
最近幾年，粒子方法出現了又一些新的發展，一領域用傳統的分析方法解決不了的問題，現在可以藉助基於粒子仿真的方法來解決．在動態系統的模型選擇，故障檢測、診斷方面，出現了基於粒子的假設檢驗、粒子多模型、粒子似然度比檢測等方法．在參數估計方面，通常把靜止的參數作為擴展的狀態向量的一部分，但是由於參數是靜態的，粒子會很快退化成一個樣本，為避免退化，常用的方法有給靜參數人為增加動態噪聲_9 以及Kernel平滑方法 ，而Doucet等提出的點估計方法避免對參數直接採樣，在粒子框架下使用最大似然估計(ML)以及期望值最大(EM)算法直接估計未知參數 ．在隨機最佳化方面，出現了基於粒子方法的梯度估計算法，使得粒子方法也用於最優控制等領域．Andrieu，Doucet等在文獻[70]中詳細回顧了粒子方法在變化檢測、系統辨識和控制中的套用及理論上的一些最新進展，許多僅僅在幾年前不能解決的問題現在可以求助於這種基於仿真的粒子方法．
總結與展望(Summarization and prospect)
目前粒子濾波器的研究已取得許多可喜的進展，套用範圍也由濾波估計擴展到新的領域，作為一種新方法，粒子方法還處於發展之中，還存在許多有待解決的問題，例如隨機採樣帶來Monte Carlo誤差的積累甚至導致濾波器發散、為避免退化和提高精度而需要大量的粒子使得計算量急劇增加、粒子方法是否是解決非線性非高斯問題的萬能方法還值得探討．此外粒子濾波器還只是停留在仿真階段，全面考慮實際中的各種因素也是深化PF研究不可缺少的一個環節．儘管如此，在一些精度要求高而經典的分析方法又解決不了的場合，這種基於仿真的逼近方法發揮了巨大潛力，而現代計算機和並行計算技術的迅速發展又為粒子方法的發展和套用提供了有力支持，相信粒子濾波器的研究將朝著更深，更廣的方向發展．
粒子濾波發展
MCMC改進策略
馬爾可夫鏈蒙特卡洛(MCMC)方法通過構造Markov鏈，產生來自目標分布的樣本，並且具有很好的收斂性。在SIS的每次疊代中，結合MCMC使粒子能夠移動到不同地方，從而可以避免退化現象，而且Markov鏈能將粒子推向更接近狀態機率密度函式(probability density function,(PDF))的地方，使樣本分布更合理。基於MCMC改進策略的方法有許多，常用的有Gibbs採樣器和MetropolisHasting方法。
Unscented粒子濾波器(UPF)
Unscented Kalman濾波器(UKF)是Julier等人提出的。EKF(Extended Kalman Filter)使用一階Taylor展開式逼近非線性項，用高斯分布近似狀態分布。UKF類似於EKF，用高斯分布逼近狀態分布，但不需要線性化只使用少數幾個稱為Sigma點的樣本。這些點通過非線性模型後，所得均值和方差能夠精確到非線性項Taylor展開式的二階項，從而對非線性濾波精度更高。Merwe等人提出使用UKF產生PF的重要性分布，稱為Unscented粒子濾波器(UPF)，由UKF產生的重要性分布與真實狀態PDF的支集重疊部分更大，估計精度更高。
Rao－Blackwellised粒子濾波器(RBPF)
在高維狀態空間中採樣時,PF的效率很低。對某些狀態空間模型，狀態向量的一部分在其餘部分的條件下的後驗分布可以用解析方法求得，例如某些狀態是條件線性高斯模型，可用Kalman濾波器得到條件後驗分布，對另外部分狀態用PF，從而得到一種混合濾波器，降低了PF採樣空間的維數，RBPF樣本的重要性權的方差遠遠低於SIR方法的權的方差，為使用粒子濾波器解決 SLAM問題提供了理論基礎。而Montemerlo等人在2002年首次將Rao-Blackwellised粒子濾波器套用到機器人SLAM中，並取名為FastSLAM算法。該算法將SLAM問題分解成機器人定位問題和基於位姿估計的環境特徵位置估計問題，用粒子濾波算法做整個路徑的位置估計，用EKF估計環境特徵的位置，每一個EKF對應一個環境特徵。該方法融合EKF和機率方法的優點，既降低了計算的複雜度，又具有較好的魯棒性。
