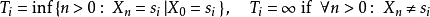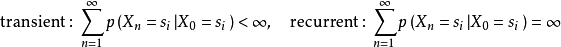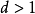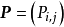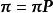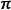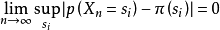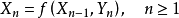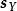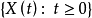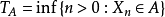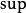歷史 馬爾可夫鏈的提出來自俄國數學家
安德雷·馬爾可夫 (Андрей Андреевич Марков)。馬爾可夫在1906-1907年間發表的研究中為了證明隨機變數間的獨立性不是
弱大數定律 (weak law of large numbers)和
中心極限定理 (central limit theorem)成立的必要條件,構造了一個按條件機率相互依賴的
隨機過程 ,並證明其在一定條件下收斂於一組向量,該隨機過程被後世稱為馬爾可夫鏈。
在馬爾可夫鏈被提出之後,
保羅·埃倫費斯特 (Paul Ehrenfest)和Tatiana Afanasyeva在1907年使用馬爾可夫鏈建立了Ehrenfest擴散模型(Ehrenfest model of diffusion)。1912年
亨利·龐加萊 (Jules Henri Poincaré)研究了
有限群 上的馬爾可夫鏈並得到了
龐加萊不等式 (Poincaré inequality)。
1931年,
安德雷·柯爾莫哥洛夫 (Андрей Николаевич Колмогоров)在對擴散問題的研究中將馬爾可夫鏈推廣至連續指數集得到了連續時間馬爾可夫鏈,並推出了其聯合分布函式的計算公式。獨立於柯爾莫哥洛夫,1926年,Sydney Chapman在研究
布朗運動 時也得到了該計算公式,即後來的Chapman-Kolmogorov等式。二十世紀50年代,前蘇聯數學家
Eugene Borisovich Dynkin 完善了柯爾莫哥洛夫的理論並通過Dynkin公式(Dynkin formula)將平穩馬爾可夫過程與
鞅過程 (martingale process)相聯繫。此後以馬爾可夫鏈和馬爾可夫過程為基礎,各類馬爾可夫模型被相繼提出並在實際問題中得到套用了。
定義 馬爾可夫鏈是一組具有馬爾可夫性質的離散隨機變數的集合。具體地,對
機率空間 內以一維
可數集 為指數集(index set) 的
隨機變數 集合
,若隨機變數的取值都在可數集內:
,且隨機變數的條件機率滿足如下關係:
則
被稱為馬爾可夫鏈,可數集
被稱為
狀態空間 (state space),馬爾可夫鏈在狀態空間內的取值稱為狀態。這裡定義的馬爾可夫鏈是離散時間馬爾可夫鏈(Discrete-Time MC, DTMC),其具有連續指數集的情形雖然被稱為
連續時間馬爾可夫鏈 (Continuous-Time MC, CTMC),但在本質上是
馬爾可夫過程 (Markov process)。常見地,馬爾可夫鏈的指數集被稱為“步”或“時間步(time-step)”。
上式在定義馬爾可夫鏈的同時定義了
馬爾可夫性質 ,該性質也被稱為“無記憶性(memorylessness)”,即t+1步的隨機變數在給定第t步隨機變數後與其餘的隨機變數條件獨立(conditionally independent):
。在此基礎上,馬爾可夫鏈具有強馬爾可夫性(strong Markov property),即對任意的
停時 ( stopping time),馬爾可夫鏈在停時前後的狀態相互獨立。
解釋性例子
馬爾科夫鏈的一個常見例子是簡化的股票漲跌模型:若一天中某股票上漲,則明天該股票有機率p開始下跌,1-p繼續上漲;若一天中該股票下跌,則明天該股票有機率q開始上漲,1-q繼續下跌。該股票的漲跌情況是一個馬爾可夫鏈,且定義中各個概念在例子中有如下對應:
隨機變數:第t天該股票的狀態;狀態空間:“上漲”和“下跌”;指數集:天數。
條件機率關係:按定義,即便已知該股票的所有歷史狀態,其在某天的漲跌也僅與前一天的狀態有關。
無記憶性:該股票當天的表現僅與前一天有關,與其他歷史狀態無關(定義條件機率關係的同時定義了無記憶性)。
停時前後狀態相互獨立:取出該股票的漲跌記錄,然後從中截取一段,我們無法知道截取的是哪一段,因為截取點,即停時t前後的記錄(t-1和t+1)沒有依賴關係。
n-階馬爾可夫鏈(n-order Markov chain)
n-階馬爾可夫鏈擁有n階的記憶性,可視為馬爾可夫鏈的推廣。類比馬爾可夫鏈的定義,n-階馬爾可夫鏈滿足如下條件:
按上式,傳統的馬爾可夫鏈可以認為是1-階馬爾可夫鏈。由馬爾可夫性質可得,將多個馬爾可夫鏈作為組元可以得到n-階的馬爾可夫鏈。
理論與性質 轉移理論 馬爾可夫鏈中隨機變數的狀態隨時間步的變化被稱為演變(evolution)或轉移(transition)。這裡介紹描述馬爾可夫鏈結構的兩種途徑,即轉移矩陣和轉移圖,並定義了馬爾可夫鏈在轉移過程中表現出的性質。
轉移機率 (transition probability)與轉移矩陣 (transition matrix)
馬爾可夫鏈中隨機變數間的條件機率可定義為如下形式的(單步)
轉移機率 和n-步轉移機率:
式中下標
表示第n步的轉移。由馬爾可夫性質可知,在給定初始機率
後,轉移機率的連續乘法可以表示馬爾可夫鏈的有限維分布(finite-dimensional distribution):
式中的
為樣本軌道(sample path),即馬爾可夫鏈每步的取值。對n-步轉移機率,由Chapman–Kolmogorov等式可知,其值為所有樣本軌道的總和:
上式表明,馬爾可夫鏈直接演變n步等價於其先演變n-k步,再演變k步(k處於該馬爾可夫鏈的狀態空間內)。n-步轉移機率與初始機率的乘積被稱為該狀態的絕對機率。
若一個馬爾可夫鏈的
狀態空間 是有限的,則可在單步演變中將所有狀態的轉移機率按矩陣排列,得到轉移矩陣:
馬爾可夫鏈的轉移矩陣是右隨機矩陣(right stochastic matrix),矩陣的第
行表示
時
取所有可能狀態的機率(
離散分布 ),因此馬爾可夫鏈完全決定轉移矩陣,轉移矩陣也完全決定馬爾可夫鏈。由機率分布的性質可得,轉移矩陣是一個
正定矩陣 ,且每行元素之和等於1:
按相同的方式也可定義n-步轉移矩陣:
,由n-步轉移機率的性質(Chapman–Kolmogorov等式)可知,n-步轉移矩陣是其之前所有轉移矩陣的連續矩陣乘法:
。
轉移圖(transition graph)
1. 可達(accessible)與連通(communicate)
馬爾可夫鏈的演變可以按
圖 (graph)結構,表示為轉移圖(transition graph),圖中的每條邊都被賦予一個轉移機率。通過轉移圖可引入“可達”和“連通”的概念:
若對馬爾可夫鏈中的狀態
有:
,即採樣路徑上的所有轉移機率不為0,則狀態
是狀態
的可達狀態,在轉移圖中表示為有向連線:
。如果
互為可達狀態,則二者是連通的,在轉移圖中形成閉合迴路,記為
。由定義,可達與連通可以是間接的,即不必在單個時間步完成。
連通是一組等價關係,因此可以構建
等價類 (equivalence classes),在馬爾可夫鏈中,包含儘可能多狀態的等價類被稱為連通類(communicating class)。
2. 閉合集(closed set)與吸收態(absorbing state)
給定狀態空間的一個子集,若馬爾可夫鏈進入該子集後無法離開:
,則該子集是閉合的,稱為閉合集,一個閉合集外部的所有狀態都不是其可達狀態。若閉合集中只有一個狀態,則該狀態是吸收態,在轉移圖中是一個機率為1的自環。一個閉合集可以包括一個或多個連通類。
3. 轉移圖的例子
這裡通過一個轉移圖的例子對上述概念進行舉例說明:
轉移圖的例子 由定義可知,該轉移圖包含了三個連通類:
、三個閉合集:
和一個吸收態,即狀態6。注意到,在上述轉移圖中,馬爾可夫鏈從任意狀態出發最終都會進入吸收態,這類馬爾可夫鏈被稱為吸收馬爾可夫鏈(absorbing Markov chain)。
性質 這裡對馬爾可夫鏈的4個性質:不可約性、重現性、周期性和遍歷性進行定義。與馬爾可夫性質不同,這些性質不是馬爾可夫鏈必然擁有的性質,而是其在轉移過程中對其狀態表現出的性質。上述性質都是排他的,即不具有可約性的馬爾可夫鏈必然是不可約的,以此類推。
周期為3的不可約馬爾可夫鏈 不可約性(irreducibility)
如果一個馬爾可夫鏈的狀態空間僅有一個連通類,即狀態空間的全體成員,則該馬爾可夫鏈是不可約的,否則馬爾可夫鏈具有可約性(reducibility)。馬爾可夫鏈的不可約性意味著在其演變過程中,隨機變數可以在任意狀態間轉移。
重現性(recurrence)
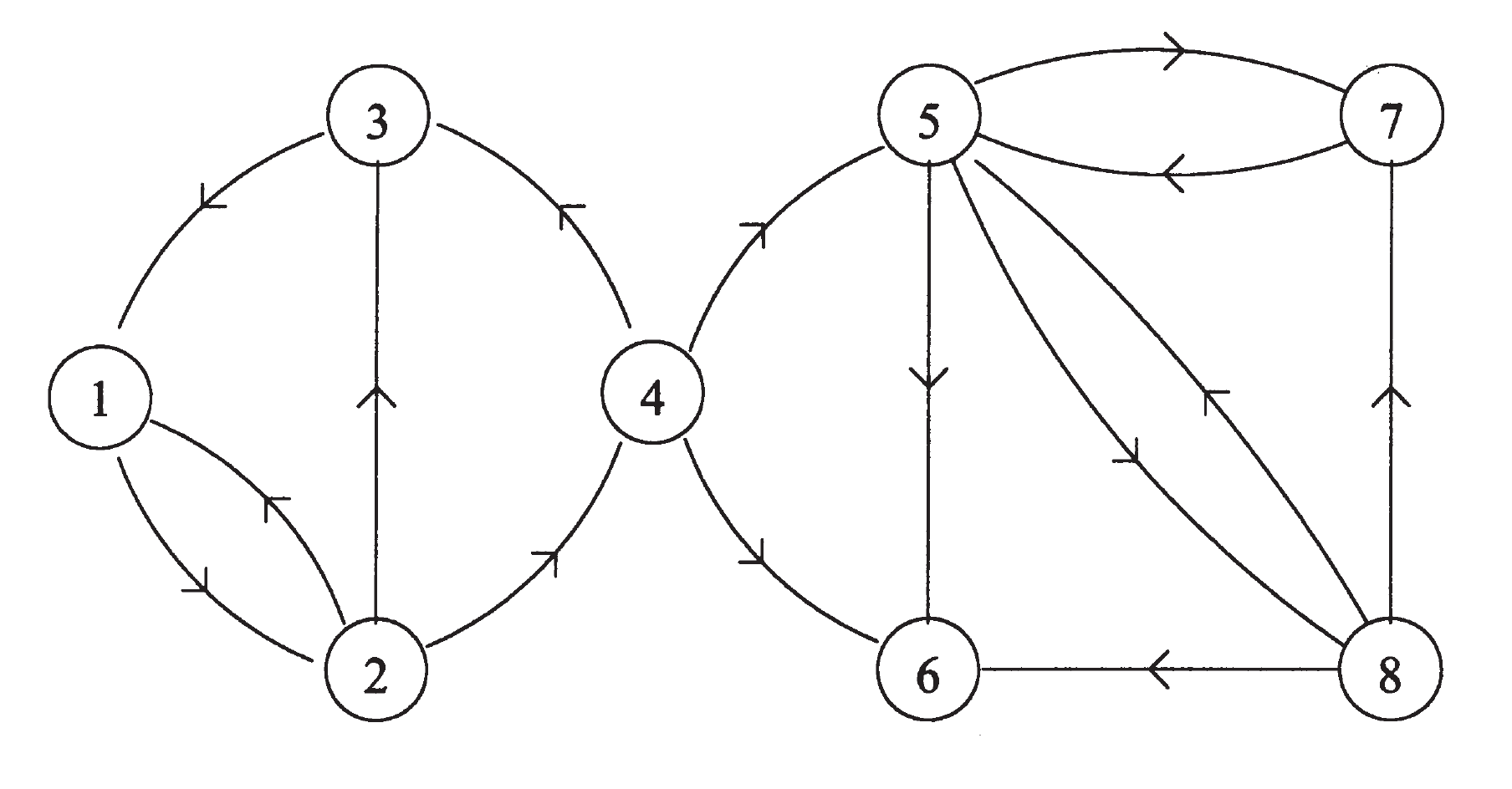
若馬爾可夫鏈在到達一個狀態後,在演變中能反覆回到該狀態,則該狀態具有重現性,或該馬爾可夫鏈具有(局部)重現性,反之則具有瞬變性(transience)的。正式地,對狀態空間中的某個狀態,馬爾可夫鏈對一給定狀態的返回時間(return time)是其所有可能返回時間的
下確界 (infimum):
若
,則該狀態不存在瞬變性或重現性的;若
,則該狀態的瞬變性和重現性的判斷準則如下:
在時間步趨於無窮時,可重現狀態的返回機率(return probability)的和,即總訪問次數的期望也趨於無窮:
此外,若狀態
具有重現性,則可計算其平均重現時間(mean recurrence time):
若平均重現時間
,該狀態是“正重現的(positive recurrent)”,否則為“零重現的(null recurrent)”。若一個狀態是零重現的,那意味著馬爾可夫鏈兩次訪問該狀態的時間間隔的期望是正無窮。
由上述瞬變性和重現性的定義可有如下推論:
推論 :對有限個狀態的馬爾可夫鏈,其至少有一個狀態是可重現的,且所有可重現狀態都是正可重現的。
推論 :若有限個狀態的馬爾可夫鏈是不可約的,則其所有狀態是正重現的。
推論 :若狀態A是可重現的,且狀態B是A的可達狀態,則A與B是連通的,且B是可重現的。
推論 :若狀態B是A的可達狀態,且狀態B是吸收態,則B是可重現狀態,A是瞬變狀態。
推論 :由正可重現狀態組成的集合是閉合集,但閉合集中的狀態未必是可重現狀態。
周期性(periodicity)
一個正重現的馬爾可夫鏈可能具有周期性,即在其演變中,馬爾可夫鏈能夠按大於1的周期重現其狀態。正式地,給定具有正重現性的狀態
,其重現周期按如下方式計算:
式中
表示取集合元素的
最大公約數 。舉例說明,若在轉移圖中,一個馬爾可夫鏈重現某狀態需要的步數為
,則其周期是3,即重現該狀態所需的最小步數。若按上式計算得到
,該狀態具有周期性,若
,該狀態具有非周期性(aperiodicity)。由周期性的定義可有如下推論:
推論 :吸收態是非周期性狀態。
推論 :若狀態A與狀態B連通,則A與B周期相同。
推論 :若不可約的馬爾可夫鏈有周期性狀態A,則該馬爾可夫鏈的所有狀態為周期性狀態。
遍歷性(ergodicity)
若馬爾可夫鏈的一個狀態是正重現的和非周期的,則該狀態具有遍歷性。若一個馬爾可夫鏈是不可還原的,且有某個狀態是遍歷的,則該馬爾可夫鏈的所有狀態都是遍歷的,被稱為遍歷鏈。由上述定義,遍歷性有如下推論:
推論 :若狀態A是吸收態,且A是狀態B的可達狀態,則A是遍歷的,B不是遍歷的。
推論 :若多個狀態的馬爾可夫鏈包含吸收態,則該馬爾可夫鏈不是遍歷鏈。
推論 :若多個狀態的馬爾可夫鏈形成有向無環圖,或單個閉環,則該馬爾可夫鏈不是遍歷鏈。
遍歷鏈是非周期的平穩馬爾可夫鏈,有長時間尺度下的穩態行為,因此是被廣泛研究和套用的馬爾可夫鏈。
穩態分析 這裡介紹馬爾可夫鏈的長時間尺度行為的描述,即平穩分布和極限分布,並定義平穩馬爾可夫鏈。
平穩分布(stationary distribution )
給定一個馬爾可夫鏈,若在其狀態空間存在機率分布
,且該分布滿足以下條件:
則
是該馬爾可夫鏈的平穩分布。式中
是轉移矩陣和轉移機率,等價符號右側的線性方程組被稱為平衡方程(balance equation)。進一步地,若馬爾可夫鏈的平穩分布存在,且其初始分布是平穩分布,則該馬爾可夫鏈處於穩態(steady state)。從幾何觀點,考慮馬爾可夫鏈的平穩分布有
,因此該分布的支撐集是一個正單純形(standard simplex)。
對不可約的馬爾可夫鏈,若且唯若其存在唯一平穩分布,即平衡方程
在正單純形上有唯一解時,該馬爾可夫鏈是正重現的,且平穩分布有如下表示:
上述結論被稱為平穩分布準則(stationary distribution criterion)。對不可約和可重現的馬爾可夫鏈,求解平衡方程可得到除尺度外唯一的特徵向量,即
不變測度 (invariant measure),若該馬爾可夫鏈是正重現的,則其平穩分布是求解平衡方程時得到的,特徵值為1時的特徵向量,即歸一化後的不變測度,因此馬爾可夫鏈存在平穩分布的充要條件是其存在正重現狀態。此外通過舉例可知,若一個馬爾可夫鏈包含多個由正重現狀態組成的連通類(由性質可知它們都是閉合集,所以該馬爾可夫鏈不是正重現的),則每個連通類都擁有一個平穩分布,且演變得到的穩態取決於初始分布。
極限分布 (limiting distribution) 若一個馬爾可夫鏈的狀態空間存在機率分布
並滿足如下關係:
則該分布是馬爾可夫鏈的極限分布。注意到極限分布的定義與初始分布無關,即對任意的初始分布,當時間步趨於無窮時,隨機變數的機率分布趨於極限分布。按定義,極限分布一定是平穩分布,但反之不成立,例如周期性的馬爾可夫鏈可能具有平穩分布,但周期性馬爾可夫鏈不收斂於任何分布,其平穩分布不是極限分布。
1. 極限定理(limiting theorem)
兩個獨立的非周期平穩馬爾可夫鏈,即遍歷鏈如果有相同的轉移矩陣,那么當時間步趨於無窮時,兩者極限分布間的差異趨於0。按隨機過程中的耦合(coupling)理論,該結論的表述為:對狀態空間相同的遍歷鏈
,給定任意初始分布後有:
式中
表示
上確界 (supremum)。考慮平穩分布的性質,該結論有推論:對遍歷鏈
,當時間步趨於無窮時,其極限分布趨於平穩分布:
該結論有時被稱為馬爾可夫鏈的極限定理(limit theorem of Markov chain),表明若馬爾可夫鏈是遍歷的,則其極限分布是平穩分布。對一個不可約和非周期的馬爾可夫鏈,其是遍歷鏈等價於其極限分布存在,也等價於其平穩分布存在。
2. 遍歷定理(ergodic theorem)
若一個馬爾可夫鏈為遍歷鏈,則由遍歷定理,其對某一狀態的訪問次數與時間步的比值,在時間步趨於無窮時趨近於平均重現時間的倒數,即該狀態的平穩分布或極限分布:
遍歷定理的證明依賴於
強大數定律 (Strong Law of Large Numbers, SLLN),表明遍歷鏈無論初始分布如何,在經過足夠長的演變後,對其中一個隨機變數進行多次觀測(極限定理)和對多個隨機變數進行一次觀測(上式左側)都可以得到極限分布的近似。由於遍歷鏈滿足極限定理和遍歷定理,因此MCMC通過構建遍歷鏈以確保其在疊代中收斂於平穩分布。
平穩馬爾可夫鏈(stationary Markov chain)
若一個馬爾可夫鏈擁有唯一的平穩分布且極限分布收斂於平穩分布,則按定義等價於,該馬爾可夫鏈是平穩馬爾可夫鏈。平穩馬爾可夫鏈是嚴格
平穩隨機過程 ,其演變與時間順序無關:
由極限定理可知,遍歷鏈是平穩馬爾可夫鏈。此外由上述定義,平穩馬爾可夫鏈的轉移矩陣是常數矩陣,n-步轉移矩陣則是該常數矩陣的n次冪。平穩馬爾可夫鏈也被稱為齊次馬爾可夫鏈(time-homogeneous Markov chain)與之對應的,若馬爾可夫鏈不滿足上述條件,則被稱為非平穩馬爾可夫鏈(non-stationary Markvo chain)或非齊次馬爾可夫鏈(time-inhomogeneous Markov chain)。
若平穩馬爾可夫鏈對其任意兩個狀態滿足
細緻平衡 (detailed balance)條件,則其具有可逆性,被稱為
可逆馬爾可夫鏈 (reversible Markov chain) :
馬爾可夫鏈的可逆性是更嚴格的不可約性,即其不僅可以在任意狀態間轉移,且向各狀態轉移的機率是相等的,因此可逆馬爾可夫鏈是平穩馬爾可夫鏈的充分非必要條件。在馬爾可夫鏈蒙特卡羅(Markvo chain Monte Carlo, MCMC) 中,構建滿足細緻平衡條件的可逆馬爾可夫鏈,是確保其以採樣分布為平穩分布的方法。
特例 伯努利過程 (Bernoulli process)
伯努利過程也被稱為二項馬可夫鏈(Binomial Markov chain),其建立過程如下:給定一系列相互獨立的“標識”,每個標識都是二項的,按機率
取正和負。令正隨機過程
表示n個標識中有k個正標識的機率,則其是一個伯努利過程,其中的隨機變數服從二項分布(binomial distribution):
由建立過程可知,增加的新標識中正標識的機率與先前正標識的數量無關,具有馬爾可夫性質,因此伯努利過程是一個馬爾可夫鏈。
賭徒破產問題(gambler's ruin)
假設賭徒持有有限個籌碼在賭場下注,每次下注以機率
贏或輸一個籌碼,若賭徒不斷下注,則其持有的籌碼總數是一個馬爾可夫鏈,且有如下轉移矩陣:
賭徒輸光籌碼是吸收態,由一步分析(one-step analysis)可知,當
時,該馬爾可夫鏈必然進入吸收態,即賭徒無論持有多少籌碼,隨著賭注的進行最終都會輸光。
隨機遊走 (random walk)
定義一系列獨立同分布(independent identically distributed, iid)的整數隨機變數
,並定義如下隨機過程:
則隨機過程
是整數集內的隨機遊走,而
是步長。由於步長是iid的,因此當前步與先前步相互獨立,該隨機過程是馬爾可夫鏈。伯努利過程和賭徒破產問題都是隨機遊走的特例。
由上述隨機遊走的例子可知,馬爾可夫鏈有一般性的構建方法,具體地,若狀態空間
內的隨機過程
有滿足形式:
其中,
,
為空間
的iid隨機變數且獨立於
,則隨機過程
是馬爾可夫鏈,其一步轉移機率為:
。該結論表明,馬爾可夫鏈可以由
區間內服從iid均勻分布的隨機變數(隨機數)進行數值模擬。
推廣
馬爾可夫過程(Markov process)
馬爾可夫過程也被稱為連續時間馬爾可夫鏈,是馬爾可夫鏈或離散時間馬爾可夫鏈的推廣,其狀態空間是可數集,但一維指數集不再有可數集的限制,可以表示連續時間。馬爾可夫過程與馬爾可夫鏈的性質是可以類比的,其馬爾可夫性質通常有如下表示:
由於馬爾可夫過程的狀態空間是可數集,在連續時間下其樣本軌道幾乎必然(a.s.)是
右連續 的片段函式,因此馬爾可夫過程可以表示為跳躍過程(jump process)並與馬爾可夫鏈相聯繫:
式中
是某個狀態的滯留時間(sojourn time),
是順序的指數集成員(時間片段)。滿足上述關係的馬爾可夫鏈
和滯留時間
是跳躍過程
在有限個時間片段下的局部嵌入過程(locally embedded process)。
馬爾可夫模型(Markov model )
馬爾可夫鏈或馬爾可夫過程不是唯一以馬爾可夫性質為基礎建立的隨機過程,事實上,
隱馬爾可夫模型 、
馬爾可夫決策過程 、
馬爾可夫隨機場 等隨機過程/隨機模型都具有馬爾可夫性質並被統稱為馬爾可夫模型。這裡對馬爾可夫模型的其它成員做簡要介紹:
1. 隱馬爾可夫模型(Hidden Markov Model, HMM)
HMM是一個狀態空間不完全可見,即包含隱藏狀態(hidden status)的馬爾可夫鏈,HMM中可見的部分被稱為輸出狀態(emission state),與隱藏狀態有關,但不足以形成完全的對應關係。以
語音識別 (speech recognition)為例,需要識別的語句是不可見的隱藏狀態,接收的語音或音頻是和語句有關的輸出狀態,此時HMM常見的套用是基於馬爾可夫性質從語音輸入推出其對應的語句,即從輸出狀態反解隱藏狀態。
2. 馬爾可夫決策過程(Markov decision process, MDP) :
MDP是在狀態空間的基礎上引入了“動作”的馬爾可夫鏈,即馬爾可夫鏈的轉移機率不僅與當前狀態有關,也與當前動作有關。MDP的一個例子是下棋,智慧型體對下一步棋的決策取決於當前的盤面和對手當前的動作,其中決策(policy)是狀態到動作的映射。MDP是
強化學習 (reinforcement learning)方法的重要實現,被用於計算決策所得到的“回報”,即值函式(value function)。
深度強化學習 是使用
深度學習 (deep learning)方法求解值函式極大值所對應決策的最佳化過程。MDP的推廣之一是
部分可觀察馬爾可夫決策過程 (partially observable Markov decision process, POMDP),即考慮了HMM中隱藏狀態和輸出狀態的MDP。
3. 馬爾可夫隨機場(Markov Random Field, MRF)
MRF是馬爾可夫鏈由一維指數集向高維空間的推廣。MRF的馬爾可夫性質表現為其任意一個隨機變數的狀態僅由其所有鄰接隨機變數的狀態決定。 類比馬爾可夫鏈中的有限維分布,MRF中隨機變數的聯合機率分布是所有包含該隨機變數的團(cliques)的乘積。MRF最常見的例子是
伊辛模型 (Ising model)。
哈里斯鏈(Harris chain)
哈里斯鏈是馬爾可夫鏈從可數狀態空間向連續狀態空間的推廣,給定可測空間
上的平穩馬爾可夫鏈
,若對可測空間的任意子集
和子集的返回時間
,該馬爾可夫鏈滿足:
則該馬爾可夫鏈是哈里斯可重現(Harris recurrent)的,被稱為哈里斯鏈,式中的
是可測空間的σ-有限測度(σ-finite measure)。
套用 MCMC 構建以採樣分布為極限分布的馬爾可夫鏈是馬爾可夫鏈蒙特卡羅(Markov Chain Monte Carlo, MCMC)的核心步驟,MCMC通過在馬爾可夫鏈上運行大量的時間步得到近似服從採樣分布的隨機數,並使用這些隨機數逼近求解目標對採樣分布的數學期望:
馬爾可夫鏈的極限分布性質決定了MCMC是
無偏估計 (unbiased estimation),即採樣數趨於無窮時會得到求解目標數學期望的真實值,這將MCMC與其替代方法,例如
變分貝葉斯估計 (variational Bayesian inference)相區分,後者計算量通常小於MCMC但無法得到無偏估計。
其它 在物理學和化學中,馬爾可夫鏈和馬爾可夫過程被用於對
動力系統 進行建模,形成了馬爾可夫動力學(Markov dynamics)。 在
排隊論 (queueing theory)中,馬爾可夫鏈是排隊過程的基本模型。在信號處理方面,馬爾可夫鏈是一些序列數據壓縮算法,例如Ziv-Lempel編碼的數學模型,在金融領域,馬爾可夫鏈模型被用於預測企業產品的市場占有率。

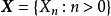


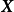













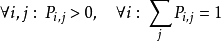
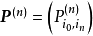
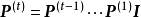



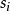




 轉移圖的例子
轉移圖的例子
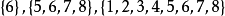
 周期為3的不可約馬爾可夫鏈
周期為3的不可約馬爾可夫鏈