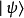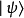量子馬爾可夫鏈

量子馬爾可夫鏈為一數學名詞，是經典馬爾可夫鏈的變體，將經典機率替換成量子機率（Quantum probability）。粗略來說，量子馬爾可夫鏈理論類似於量子有限自動機（Quantum_finite_automata），但是包含一些特殊的特性：比如，初始矩陣是一個密度矩陣，而且規則運算元變成了正運算元值測量（英語：POVM）。

基本介紹

• 中文名：量子馬爾可夫鏈
• 外文名：Quantum Markov chain

簡介

量子馬爾可夫鏈用來描述量子系統的動態演化，其中量子遊走是一類特殊的量子馬爾可夫鏈 ，已經成功套用於設計和分析量子算法。文獻定義了量子馬爾可夫鏈 ，它適合於量子密鑰協定等 ，其中量子效應被編碼為超運算元用來標籤狀態轉移 ，狀態採用經典邏輯來刻畫 ，最後提出了檢測算法。該量子馬爾可夫鏈的模型檢測是機率計算樹邏輯的量子推廣。文獻利用 Bottom 強連通分支（BSCC）和運算元漸近平均值提出了計算量子馬爾可夫鏈的可達性 、重複可達性 、一致可達性機率的方法。量子馬爾可夫鏈線性時間屬性還未得到充分研究 ，特別是量子安全性和量子不變性的檢測 ，因此開展這方面工作是有意義的。

形式定義

更準確的來說，量子馬爾可夫鏈是一組，其中為密度矩陣，為量子通道（quantum channel），可以使

為一個全正保跡（completely positive trace-preserving）映射，且為有界子的C*-代數，必須滿足以下的量子馬爾可夫條件，也就是

針對所有 。

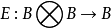
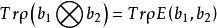
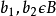
Exogenous 量子馬爾可夫鏈

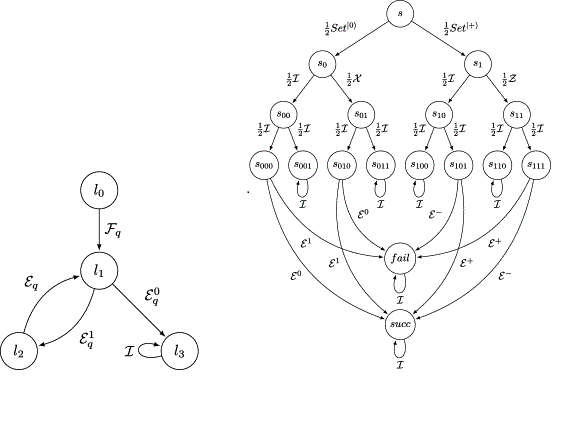
量子馬爾可夫鏈已經被學者們所研究,它主要用來刻畫量子系統的動態演化。量子行走是一類特殊的量子馬爾可夫鏈，得到廣泛關注,已經成功套用於設計和分析量子算法。文獻將量子馬爾可夫鏈定義為二元組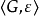，G 是有向圖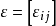，是遷移運算元矩陣(TOM)。矩陣 TOM 的每一個元素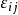標籤為點 i 到點 j 的邊,它滿足完全正性，且每列的和為一個量子運算。該量子馬爾可夫鏈給出量子系統狀態轉移的特性，每一個節點代表一個狀態，但狀態是經典的且狀態數是有限的，而量子系統的狀態是用量子態描述且 Hilbert 空間是連續的。文獻將經典馬爾可夫鏈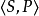推廣到量子情形，定義了量子馬爾可夫鏈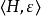，用 Hilbert 空間 H替代狀態空間 S，用超運算元 ε 替代機率轉移矩陣 P，量子狀態空間是連續的。文獻定義了量子馬爾可夫鏈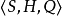，其中，S 是經典狀態集,H 是量子狀態空間，Q 表示狀態轉移運算元矩陣，該模型採用經典命題邏輯來刻畫量子系統的狀態屬性，但不是用量子邏輯刻畫量子態。

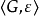
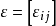
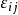
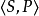
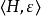
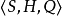
如何用量子邏輯刻畫量子馬爾可夫鏈的量子態，合適的量子邏輯是關鍵.關於量子邏輯，一般是指畢克霍夫-馮·諾依曼等學者提出的一類正交模格數學代數結構。然而，文獻提出了基於 Exogenous 的量子命題邏輯，刻畫了量子態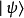的屬性，同時還保持經典命題邏輯特性。不過，Exogenous 量子命題邏輯系統只適合刻畫量子態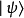，而不適合刻畫用密度運算元描述的開放量子系統。