不可約馬爾可夫鏈(irreducible Markov chain)一種馬爾可夫鏈。指狀態空間E是惟一閉集的馬爾可夫鏈,這又相當於E不含兩個不相交的非空閉集。
馬爾可夫鏈在統計物理,生物遺傳,傳染病傳播,化學高分子鏈,經濟數學等方面套用廣泛。
基本介紹
- 中文名:不可約馬爾可夫鏈
- 外文名:irreducible Markov chain
- 領域:數學
- 性質:馬爾可夫鏈
- 性質:狀態空間是唯一閉集
- 套用:統計物理、生物遺傳
概念,馬爾可夫鏈,狀態空間,人物簡介——馬爾可夫,
概念
不可約馬爾可夫鏈(irreducible Markov chain)是一種馬爾可夫鏈。指狀態空間E是惟一閉集的馬爾可夫鏈,這又相當於E不含兩個不相交的非空閉集。這時,對應的轉移機率矩陣也稱為不可約的。
馬爾可夫鏈
設{Xt(w),t∈T}是一個馬爾可夫過程,如果T={0,1,2,…},且其狀態空間是有限集合或可列集合,則稱此過程 為馬爾可夫鏈。按狀態空間所含狀態的情況, 又分為可列(狀態的)馬爾可夫鏈和有限(狀 態的)馬爾可夫鏈。馬爾可夫鏈是最簡單的馬爾可夫過程。
馬爾可夫鏈的狀態,可以指在物理化學 中一原子的某一能量水平;可以指在民意測 驗中投票人各種可能的思想狀態;可以指在 布朗運動中微粒在三維空間的位置等。如果 用不同的整數來表示這些狀態,則狀態空間可以看作是全體或部分整數組成的集合。
如果不藉助於馬爾可夫過程的概念,馬 爾可夫鏈可這樣陳述:{Xn,n=0,1,2,…}是 在整數集合I上取值的隨機變數序列,如果 對任意的非負整數t1<t2<…<t1<t,有:
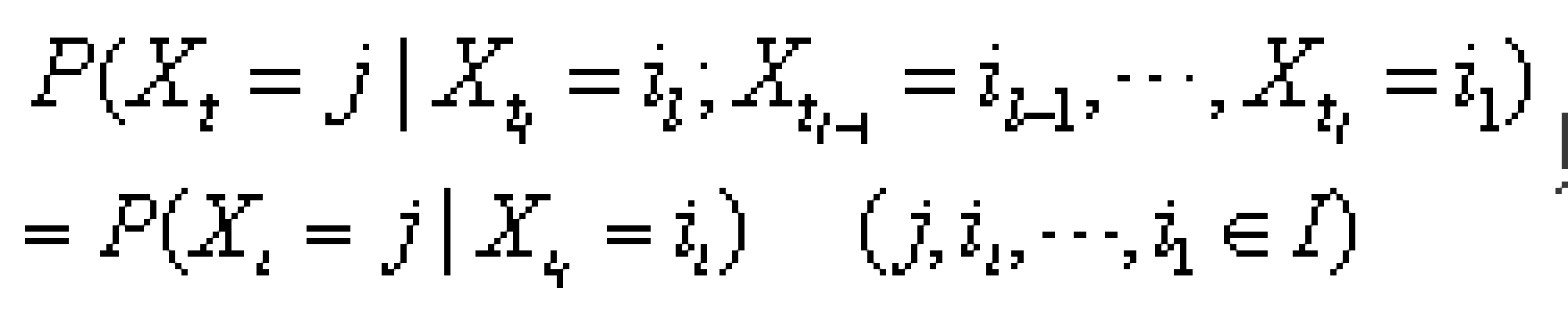
則稱此隨機序列{Xn}具有馬爾可夫性或無後效性,稱{Xn}為馬爾可夫鏈,簡稱馬氏鏈。
馬爾可夫鏈首先由馬爾可夫提出。作為 獨立試驗序列概型最簡單的推廣,馬爾可夫 提出了一種最簡單的相依試驗序列概型,這 就是早期用比較直觀的語言表述的馬爾可夫鏈,這種表述方法至今還常為人們採用。
設{Ei,(i=0,1,2,…)}為一列隨機試驗,它們的一切可能出現的試驗結果wi構成 的集合Ω={ω0,ω1,ω2,…}為有限集合或可 列集合。記第i次試驗出現的結果為w′i,如果對任意兩正整數m,k和任意整數0≤j1<j2<…<jl<m,有:
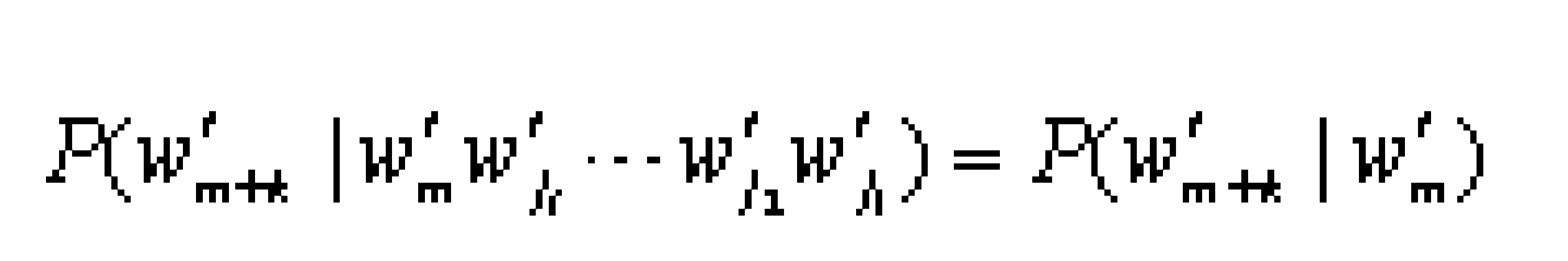
則稱隨機試驗序列{Ei,i=0,1,2,…}為馬爾可夫鏈。
顯然,上面的馬爾可夫鏈的兩種描述實 質上是完全相同的。
對於馬爾可夫鏈,描述它機率性質最重 要的是它在時刻m的一步轉移機率pij(m): pij(m)=P(Xm+1=j|Xm=i) (i,j∈I) 它表示在時刻m,Xm取值i的條件下,於下一 時刻轉移到j的機率。一般地,在時刻m的k 步轉移機率pij(m):
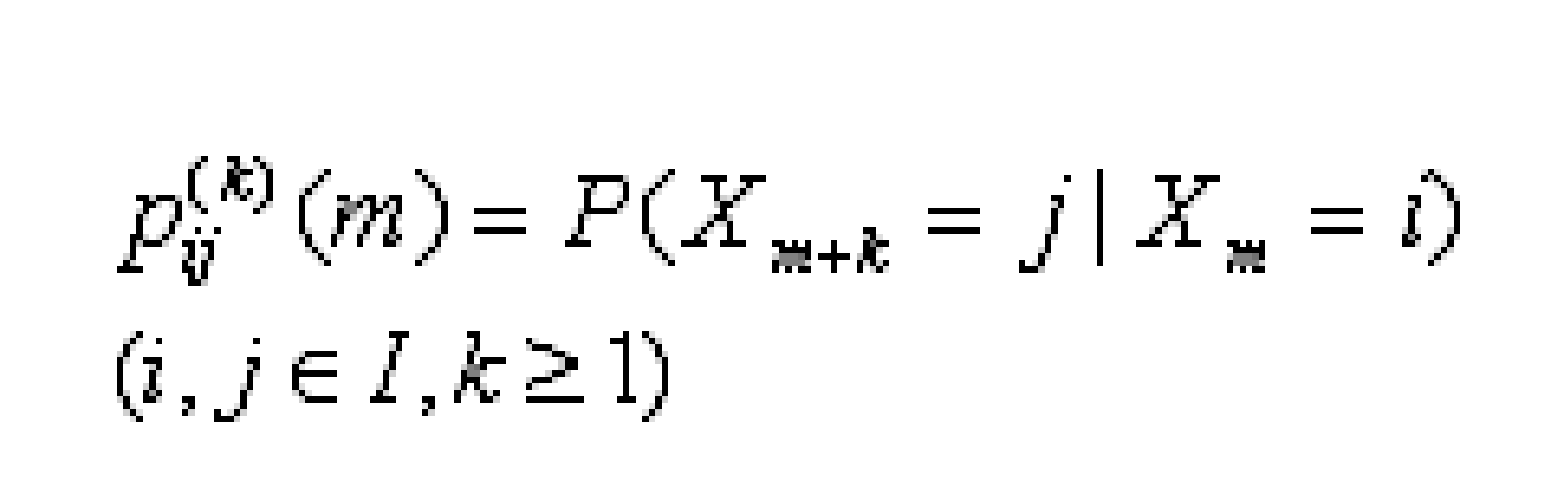
注意,pij(m)=pij(m)。由馬爾可夫性可知:
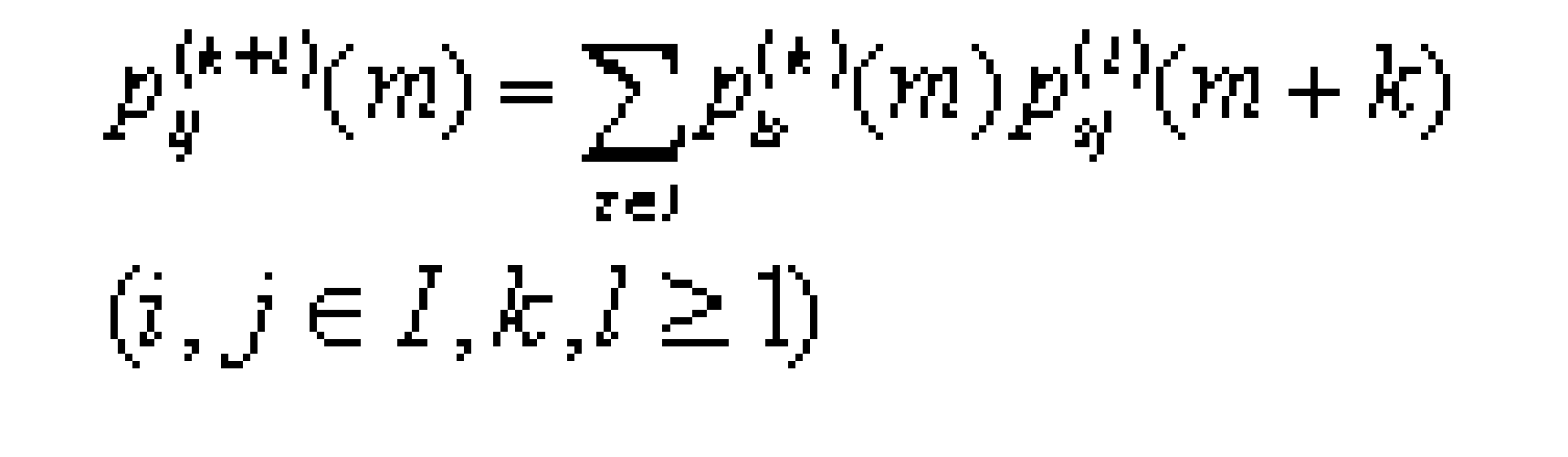
這就是切普曼——柯爾莫哥洛夫方程。
如令矩陣P(m)=(Pijm,(i,j∈I, m=0,1,2…),P(m)稱為馬爾可夫鏈在時 刻m的n步轉移矩陣,於是切普曼——柯爾莫哥洛夫方程可簡潔地表示成如下矩陣形式:

於是,由全部一步轉移機率可得所有的轉移機率,從而當初始分布P(X0=i)=pi已知 時,馬爾可夫鏈{Xn}的所有有限維分布也就知道了。

如果在各個時刻的一步轉移機率都相同 pij(m)=pij,則稱轉移機率具有時間齊次性 或齊次性,有時稱平穩性。此時馬爾可夫鏈稱 為齊次馬爾可夫鏈,其切普曼——柯爾莫哥 洛夫方程為:
記一步轉移矩陣為p=(pij),n步轉移矩陣為 p(n)=pij(n),則切普曼—柯爾莫哥洛夫方程的矩陣形式為:

於是:

因此對齊次馬爾可夫鏈,由初始分布和一步轉移機率就可得所有的有限維分布。
馬爾可夫鏈在統計物理,生物遺傳,傳染病傳播,化學高分子鏈,經濟數學等方面套用廣泛。
狀態空間
狀態空間是描述系統運動的一種抽象空間。指以系統的狀態變數為軸所張成的空間,亦即系統所有可能狀態的集合。具體為一般系統定義中能夠用於表示時間系統S⊂X×Y演化規則ρ-={ρt∶C×Xt→Y-t}和={φtt′∶C×Xtt′→C}的狀態C的集合。這時,可稱S為狀態空間C中的動態系統。
狀態空間的點稱為代表點或相點,系統運動軌跡(動力學方程的每個解)亦為狀態空間的一個點集合,稱為軌線.獨立狀態變數個數稱為狀態空間的維數,通常為非零整數0,1,2,…特別地,2維狀態空間稱為狀態平面。用狀態空間描述系統運動,可以把解析問題轉化為較直觀的幾何問題來處理,有時比較方便。
通常希望尋找為實現同一時間系統S所需的最小狀態空間,這時得到的動態系統描述稱為最小實現(參見“最小實現”)。
人物簡介——馬爾可夫
俄國數學家。生於梁贊,卒於聖彼得堡。1878年畢業於聖彼得堡大學,後留校工作。1884年獲物理數學博士學位。1886年成為教授。1896年當選為聖彼得堡科學院院士。1905年退休,同年,聖彼得堡大學授予他功勳教授稱號。馬爾可夫的主要貢獻在機率論、數論、函式逼近論和微分方程等方面。在機率論方面,他深入研究並發展了切比雪夫的矩方法,使中心極限定理的證明成為可能。他還推廣了大數律和中心極限定理的套用範圍。在1906—1912年間,馬爾可夫發表了一系列論著,提出並研究了一種能用數學分析方法研究自然過程的一般圖式,後來這種圖式被稱為馬爾可夫鏈。他的研究方法和重要發現推動了機率論的發展,特別是促進了機率論新分支——隨機過程論的發展。隨機過程論在現代科學中具有廣泛而重要的套用。一類重要的隨機過程又叫馬爾可夫過程。馬爾可夫所創建的機率論的研究方向,改變了機率論的內容,促使它成為與自然科學和技術直接有關的最重要的數學方法之一。在數論中,他解決了求已知行列式的極值二次式的難題。在數學分析中,發展了力矩理論、函式逼近論和連分式的解析理論及其套用。在數理統計和數的幾何等方面也做出了創造性的貢獻。他共發表70多種論著,其中《有限差分學》和《機率演算》已被視為經典著作。其子(小)馬爾可夫也是著名數學家。
