基本介紹
- 中文名:強大數定律
- 外文名:Strong Law of Large Numbers
- 提出者:波萊爾
- 提出時間:1909年
- 套用學科:數學
- 適用領域範圍:機率論
基本介紹

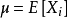



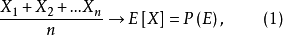

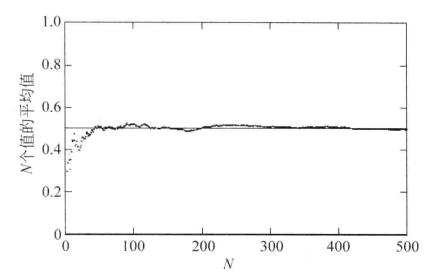 圖1強大數定律*
圖1強大數定律*弱大數定律和強大數定律的區別



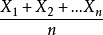


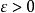

幾種常見的強大數定律
波萊爾強大數定律

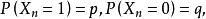
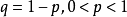
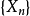
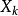



柯爾莫哥洛夫定理


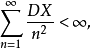

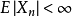


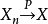
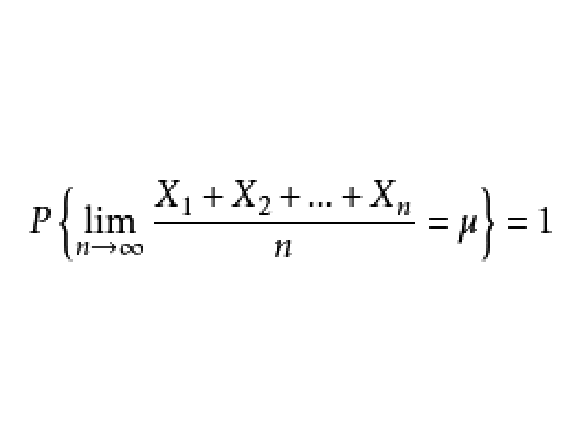

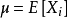



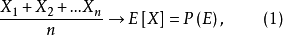

 圖1強大數定律*
圖1強大數定律*


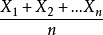


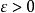


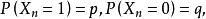
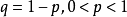
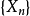
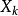





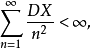

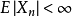


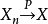
第一條強大數定律(strong law of large numbers)是由波萊爾在1909年對伯努利試驗場合驗證的,給出了幾乎處處收斂的隨機變數列的性質。強大數定律主要包括波萊爾強大數...
機率論歷史上第一個極限定理屬於伯努利,後人稱之為“大數定律”。機率論中討論隨機變數序列的算術平均值向隨機變數各數學期望的算術平均值收斂的定律。在隨機事件的...
種強大數定律,伯努利大數定律的加強。 ...... 種強大數定律,伯努利大數定律的加強。 [1] 參考資料 1. 鄭家亨,統計大辭典,中國統計出版社,1995年03月第1版,...
柯爾莫哥洛夫強大數律(Kolmogorov strong law of large numbers)是最重要最常用的強大數律。若{Xn}為獨立同分布隨機變數序列,EXn存在,則以機率1成立n個獨立同...
種強大數定律,辛欽大數定律的加強。 ...... 種強大數定律,辛欽大數定律的加強。 [1] 參考資料 1. 鄭家亨,統計大辭典,中國統計出版社,1995年03月第1版,第76...
1、董志山,楊小雲,不具有平穩分布的負相協隨機變數的強大數定律,套用機率統計,2002,Vol. 18, No. 4, 357-362。2、董志山,楊小雲,劉立新,非平穩NA隨機變數...
若具有無偏性,按照強大數定律,有這即是說,儘管一次估計的結果 (X(i))不一定恰好等於θ,但在大量重複使用時,多次估計的算術平均值可以任意接近待估參數θ的真實...
1.Borel的正軌數定理單位區間/弱大數律/強大數律/強大數律與弱大數律的對比/長度/丟番圖逼近的測度理論2.機率測度空間/指定機率/集類/機率測度/單位區間上的...
陳曉林, 吳群英, 鄧光明, 兩兩NQD的完全收斂和強大數定律, 桂林理工大學學報, 2010, 30(2): 321-323付艷莉, 吳群英, LNQD序列幾乎處處中心極限定理, 桂林...
爾莫戈洛夫公理化體系為基礎的機率論的入門讀物,內容包括:機率空間、條件機率與獨立性、隨機變數、隨機向量、隨機變數的數字特徵、特徵函式、大數定律與中心極限定理...
5.1 大數定律5.2 特徵函式5.3 中心極限定量5.4 隨機變數序列的幾種收劍性5.5 強大數定律練習題第6章 泊松信號流第7章 隨機動與馬爾可夫鏈...
《21世紀高等院校教材?套用機率論》為高等院校理工科教材,內容包括:隨機事件及其機率、隨機變數及其分布、隨機變數的數字特徵、特徵函式與機率母函式、極限定理等。《...
8.3 中心極限定理8.4 強大數定律8.5 其他不等式8.6 用泊松隨機變數逼近獨立伯努利隨機變數之和的誤差機率界小結習題理論練習自測題與練習...
