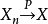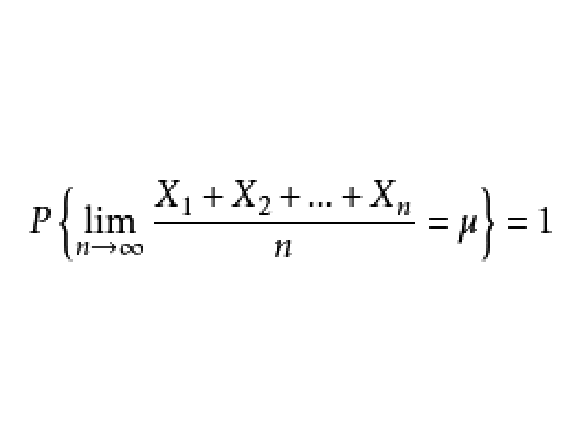強大數定律

第一條強大數定律(strong law of large numbers)是由波萊爾在1909年對伯努利試驗場合驗證的，給出了幾乎處處收斂的隨機變數列的性質。強大數定律主要包括波萊爾強大數定律、柯爾莫哥洛夫強大數定律等。 強大數定律首先由法國數學家Borel對於伯努利隨機變數的特殊情況進行證明，一般情形下的強大數定律的證明由俄國數學家柯爾莫哥洛夫(A.N.Kolmogorov)給出。

基本介紹

• 中文名：強大數定律
• 外文名：Strong Law of Large Numbers
• 提出者：波萊爾
• 提出時間：1909年
• 套用學科：數學
• 適用領域範圍：機率論

基本介紹

強大數定律可能是機率論中最廣為人知的結果，它表明了獨立同分布的隨機變數序列的均值以機率1收斂到分布的均值。

定理1 [強大數定律] 設 為一獨立同分布的隨機變數序列，其公共均值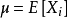 有限．則下式以機率1成立：

即強大數定律可以表達為下式：

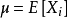
作為強大數定律的一個套用，設有一獨立重複試驗序列，令E為某一事件．P(E)為事件E發生的機率，又令

根據強大數定律，以機率1有

因為 表示在前n次試驗中事件E發生的次數，因此方程(1)說明事件E在前n次試驗中發生的頻率以機率1收斂到它的機率P(E)（關於定理的證明請參考相應書籍）。

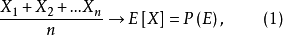
可用圖1來說明強大數定律。圖1顯示了從一個[0，1]值域內的均勻分布分別提取1，2，3，…，500個可隨機變數值，計算得到的樣本均值。該隨機分布的期望值是0.5，隨著樣本數的增加，樣本均值收斂於期望值。

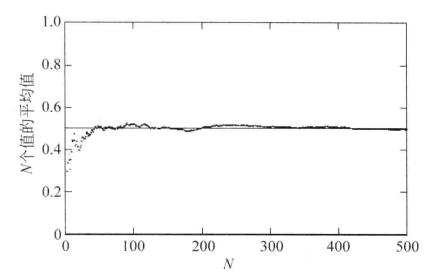圖1強大數定律*

弱大數定律和強大數定律的區別

弱大數定律表明對於足夠大的值n*，隨機變數 的值靠近 ，但它不能保證對於所有的 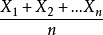， 仍停留在 附近，因此， 可以無限多次離開0(儘管出現較大偏離的頻率不會很高)。而強大數定律能保證這種情況不會發生，特別地，強大數定律表明下式以機率1成立：對任何 ，

只能出現有限次。

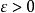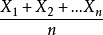
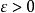
幾種常見的強大數定律

波萊爾強大數定律

定理2(波萊爾強大數定律) 設 相互獨立同分布，且

其中 ，則 服從強大數定律。

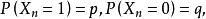
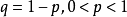
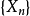
在此定理中，若令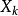 表示貝努利試驗中與第k次試驗相聯繫的隨機變數、則定理說明， 成立的機率為1。也就是說( )這一事件的機率為0(當然還不能說 必然趨於p)，從而我們進一步得到了頻率“穩定於”機率這一事實，它比貝努利大數定律有更強的結果。

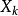
柯爾莫哥洛夫定理

定理3(柯爾莫哥洛夫判別法)設 為一相互獨立的隨機變數序列，若

則服從強大數定律。

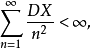
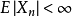定理4(柯爾莫哥洛夫定理) 設 為相互獨立同分布的隨機序列，若 ，則 服從強大數定律。

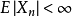
定理5 若 ，則必有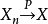 。