基本介紹
- 中文名:馬爾可夫網路
- 又稱:馬爾可夫隨機場、無向圖模型
- 定義:全聯合機率分布模型
簡介
形式化定義
- 一個函式集合 fk(也稱為因子或者團因子有時也稱為特徵),每一個 fk的定義域是圖G的團或子團k. 每一個 fk是從可能的特定聯合的指派(到元素k)到非負實數的映射。
聯合分布函式
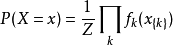
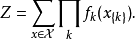
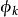
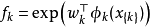
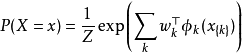
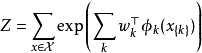
馬爾可夫性質

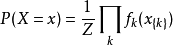
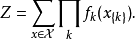
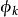
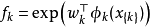
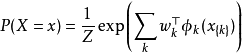
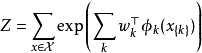

馬爾可夫網路,(馬爾可夫隨機場、無向圖模型)是關於一組有馬爾可夫性質隨機變數X的全聯合機率分布模型。...
馬爾可夫隨機場(Markov Random Field),也有人翻譯為馬爾科夫隨機場,馬爾可夫隨機場是建立在馬爾可夫模型和貝葉斯理論基礎之上的,它包含兩層意思:一是什麼是馬爾可夫,...
馬爾可夫鏈(Markov Chain, MC)是機率論和數理統計中具有馬爾可夫性質(Markov property)且存在於離散的指數集(index set)和狀態空間(state space)內的隨機過程(...
隱馬爾可夫模型(Hidden Markov Model,HMM)是統計模型,它用來描述一個含有隱含未知參數的馬爾可夫過程。其難點是從可觀察的參數中確定該過程的隱含參數。然後利用這些...
馬爾可夫決策過程(Markov Decision Process, MDP)是序貫決策(sequential decision)的數學模型,用於在系統狀態具有馬爾可夫性質的環境中模擬智慧型體可實現的隨機性策略與...
有向圖的例子包括遞歸神經網路(Recursive Neural Network)和循環神經網路(Recurrent Neural Network);無向圖的例子包括Hopfield神經網路、馬爾可夫網路(Markov Network)等...
貝葉斯網路訓練 編輯 使用貝葉斯網路必須知道各個狀態之間相關的機率。得到這些參數的過程叫做訓練。和訓練馬爾可夫模型一樣,訓練貝葉斯網路要用一些已知的數據。比如在...
《雙時間尺度的馬爾可夫系統的套用》是2013年在科學出版社出版的圖書,該書作者是]G.George Yin, Hanqin Zhang, Qinqing Zhang等。...
5.3.2不確定網路控制系統穩定性分析 5.3.3不確定網路切換控制系統穩定性分析 5.3.4網路控制系統控制器可靠性分析及容錯控制器設計 5.4基於馬爾可夫跳變系統模型...
7.1.3 一般離散動態網路和隱馬爾可夫關係 7.2 隱變數連續動態網路推理 7.2.1 模型數學描述 7.2.2 卡爾曼濾波圖模型推理 7.3 混合隱狀態動態貝葉斯網路 7....
《計算機網路數學基礎》是2014年清華大學出版社出版的圖書,作者是凱沙夫(Srinivasan...1.7.1馬爾可夫不等式241.7.2切比雪夫不等式251.7.3切諾夫限25...
5.5.3基於馬爾可夫模型描述的事件總結1535.5.4基於事件關係網路描述的事件總結153小結159中英文辭彙對照表159參考文獻159●第6章網路流量分析162...
循環神經網路(Recurrent Neural Network, RNN)是一類以序列(sequence)數據為輸入,...例如隱馬爾可夫模型(Hidden Markov Model, HMM)相結合以提升其可用性 [29-30]...
在原作者的比較試驗中,TDNN的表現超過了同等條件下的隱馬爾可夫模型(Hidden ...卷積神經網路中輸出層的上游通常是全連線層,因此其結構和工作原理與傳統前饋神經...
《天基移動通信網路》是2011年國防工業出版社出版的圖書,作者是張軍。...... 2.3 天基IP 網路多址接入協定性能分析及評估……… 73 2.3.1 協定系統的馬爾可夫...
隱馬爾可夫模型實際上是標準馬爾可夫模型的擴展,可以用λ=(A,B,π)三元組來簡潔的表示一個隱馬爾可夫模型。而因子隱馬爾科夫模型(FHMM) 是隱 Markov 模型 (...
《社會網路分析方法與實踐》是2013年機械工業出版社出版的圖書,作者是MaksimTsvet...此時,傳統的統計方法(如回歸或馬爾可夫模型)除了能解決一些瑣碎問題,在數學上變得...
《無線移動網路的移動性管理》是2005年人民郵電出版社出版的圖書,作者是朱藝華 。...... 本書對無線移動網路的移動性管理策略進行了研究,套用向量馬爾可夫過程及密度...
馬爾可夫博弈、位勢博弈、超模博弈和演化博弈,特彆強調了 重複博弈和位勢博弈的基本形式及相關性質;第3章無線網路中博弈論套用議題, 從總體上介紹了無線網路中的...
1.4隱馬爾可夫模型1.5馬爾可夫決策過程1.5.1平穩策略1.6習題第2章排隊系統與網路2.1馬爾可夫排隊系統2.1.1M/M/1/n-2排隊系統2.1.2M/M/s/n-s-1排隊系統...
馬爾可夫網路,(馬爾可夫隨機場、無向圖模型)是關於一組有馬爾可夫性質隨機變數 X的全聯合機率分布模型。 [3] 馬爾可夫網路類似貝葉斯網路用於表示依賴關係。但是,...
