置信傳播是一種在圖模型上進行推斷的訊息傳遞算法。其主要思想是：對於馬爾科夫隨機場中的每一個節點，通過訊息傳播，把該節點的機率分布狀態傳遞給相鄰的節點，從而影響相鄰節點的機率分布狀態，經過一定次數的疊代，每個節點的機率分布將收斂於一個穩態。為了使用置信傳播算法，在馬爾科夫隨機場中定義了兩個概念：訊息和置信度。
基本介紹
- 中文名：置信傳播
- 外文名：Belief Propagation（BP）
- 別名：積信息傳遞
- 提出時間：1982年
- 提出人：Pearl
- 學科：計算機科學
- 領域：數據挖掘、圖形圖像學
算法介紹,相關工具,貝葉斯網路,馬爾可夫網路,BP變形算法,基於圖模型,基於環形結構,快收斂特性,循環置信傳播,套用,
算法介紹
和 積 算 法 (Sum-Product Algorithm) 作 為 一 種 通 用 的 消 息 傳 遞 算 法(Message Passing Algorithm)，描述了因子圖中頂點（變數節點和校驗節點）處的信息計算公式，而在基於圖的編解碼系統中，我們首先需要理解的是頂點之間是如何通過邊來傳遞信息。因子圖是一種用於描述多變數函式的“二部圖”(Bipartite Graph)。一般來說，在因子圖中存在兩類節點：變數節點和對應的函式節點，變數節點所代表的變數是函式節點的自變數。同類節點之間沒有邊直接相連。
置信傳播，又名和-積信息傳遞，是一種在圖模型上進行推斷的訊息傳遞算法，可用在貝葉斯網路和馬爾科夫隨機域中。置信傳播由Pearl在1982年最早提出，後來由早期在樹上的建模推廣至在polytree上的套用。
置信傳播算法利用結點與結點之間相互傳遞信息而更新當前整個MRF（馬爾科夫隨機場）的標記狀態，是基於MRF的一種近似計算。該算法是一種疊代的方法，可以解決機率圖模型機率推斷問題，而且所有信息的傳播可以並行實現。經過多次疊代後，所有結點的信度不再發生變化，就稱此時每一個結點的標記即為最優標記，MRF也達到了收斂狀態。對於無環環路的MRF，BP算法可以收斂到其最優解。
BP算法的兩個關鍵過程：（1）通過加權乘積計算所有的局部訊息；（2）節點之間機率訊息在隨機場中的傳遞。如果X = {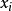
}是一組離散隨機變數聯合分布函式 p，單個變數X的邊緣分布，只是p對所有其他變數的總和：
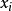
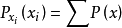
通過利用polytree結構，置信傳播可以更有效地計算邊緣。
相關工具
貝葉斯網路
貝葉斯網路（Bayesian network）是一種有效的不確定性知識表達和推理工具， 在數據挖掘等領域得到了較好的套用，又稱信念網路（belief network）或是有向無環圖模型（directed acyclic graphical model），是一種機率圖型模型，藉由有向無環圖（directed acyclic graphs, or DAGs）中得知一組隨機變數{
}及其n組條件機率分配（conditional probability distributions, or CPDs）的性質。一般而言，貝葉斯網路的有向無環圖中的節點表示隨機變數，它們可以是可觀察到的變數，抑或是隱變數、未知參數等。連線兩個節點的箭頭代表此兩個隨機變數是具有因果關係或是非條件獨立的；而兩個節點間若沒有箭頭相互連線一起的情況就稱其隨機變數彼此間為條件獨立。若兩個節點間以一個單箭頭連線在一起，表示其中一個節點是“因（parents）”，另一個是“果（descendants or children）”，兩節點就會產生一個條件機率值。比方說，我們以表示第i個節點，而的“因”以表示，的“果”表示。
貝葉斯網路（Bayesian Network）定了一個獨立的結構：一個節點的機率僅依賴於它的父節點。貝葉斯網路適用於稀疏模型，即大部分節點之間不存在任何直接的依賴關係。聯合機率（Joint Probability），表示所有節點共同發生的機率，將所有條件機率相乘。緣機率（Marginal Probability）：即某個事件發生的機率，而與其它事件無關。邊緣機率是這樣計算的：在聯合機率中，把最終結果中不需要的那些事件合併成其事件的全機率而消失（在兩個離散隨機變數的條件下，對於其中任一行或任一列求和，得到的機率就是邊緣機率）。
馬爾可夫網路
馬爾可夫網路，（馬爾可夫隨機場、無向圖模型）是關於一組有馬爾可夫性質隨機變數 X的全聯合機率分布模型。
馬爾可夫網路類似貝葉斯網路用於表示依賴關係。但是，一方面它可以表示貝葉斯網路無法表示的一些依賴關係，如循環依賴；另一方面，它不能表示貝葉斯網路能夠表示的某些關係，如推導關係。馬爾可夫網路的原型是易辛模型，最初是用來說明該模型的基本假設。
BP變形算法
基於圖模型
BP算法是一種基於樹型結構提出的漸進邊緣機率計算方法，它要求不同節點之間傳遞的外信息相互獨立。但是對於有限長LDPC碼而言，與其對應的Tanner 圖中必然會有環形結構的出現，這樣當外信息在環形結構上經過多次傳遞後，它們之間將必然產生聯繫，從而會導致錯誤信息的傳遞與疊加，進而導致 BP 算法的解碼失敗。而錯誤信息累加現象在存在較多短環時，會表現得更加明顯。綜上所述， BP 解碼算法的解碼性能較 ML 算法相比存在差距，且該差距將隨著 LDPC 碼碼長的降低而增大。因此，為了降低 BP 算法所帶來的負面作用，一方面可以藉助於碼型構造算法來減少短環出現的數量；另一方面則可以藉助於加權 BP 算法來抑制錯誤信息的疊加。
基於環形結構
有些學者首先就置信信息累加現象進行了研究，並提出了一種樹型加權 BP(Tree ReWeighted BP, TRW-BP)算法，來加強 BP 解碼算法的糾錯能力。此算法的核心思想是通過計算 Tanner 圖上成對節點間的邊在擴展樹上出現的機率(Edge Appearance Probabilities,EAPs)，並將運算結果作為加權值作用於 LLR 值的更新操作中。但 EAPs 的計算實質上是一個多維最佳化問題，本身具有相當高的計算複雜度。因此為避免 EAPs的計算， 歸一化加權 BP(Uniformly ReWeighted BP,URW-BP)算法被學者們所提出。
快收斂特性
傳統的LDPC碼BP解碼算法是分為兩步進行：首先進行全部變數點外信息的更新，然後再進行全部校驗點外信息的更新。而這種兩步解碼更新方法也被稱為擴散更新策略。研究表明，疊代過程中節點的更新策略的改變將能有效地提高解碼算法的收斂特性。比如提出的便於硬體實現的分層 BP(Layer BP, LBP)解碼算法。實驗結果表明，LBP 算法收斂速度是傳統 BP算法的兩倍。與 BP算法一樣，LBP 算法中節點的更新順序是固定的，但研究進一步指出，如果動態安排節點的更新順序，更能夠進一步地提高解碼算法的收斂速度。基於殘餘量的 BP(Residual BP, RBP)算法正是此類算法的代表。
循環置信傳播
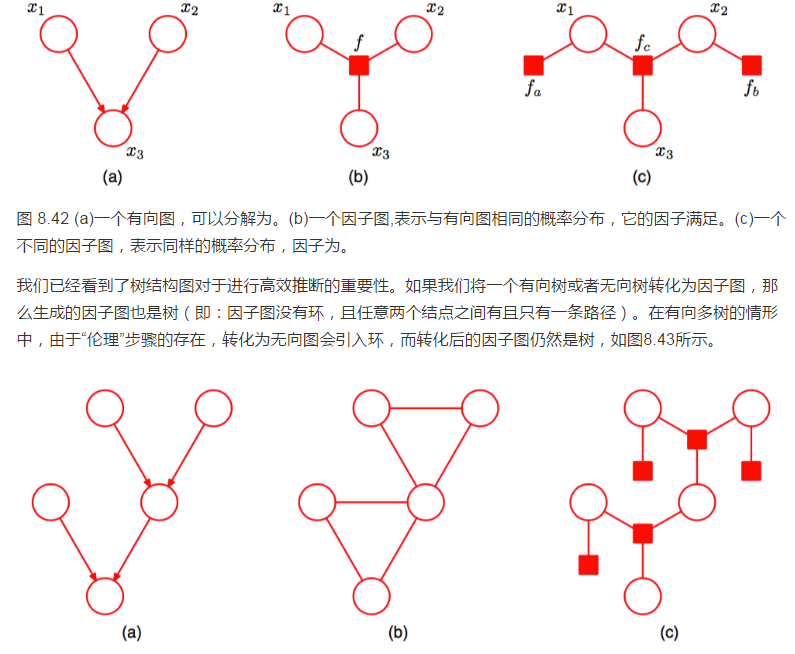
這裡，我們考慮帶有環的圖中的近似推斷的一個簡單方法，它直接依賴於之前對樹的精確推 斷的討論。主要思想就是簡單地套用加-乘算法，即使不保證能夠產生好的結果。這種方法被稱為循環置信傳播（loopy belief propagation）（Frey and MacKay，1998）。這種方法是可行的，因為加和-乘積算法的信息傳遞規則完全是局部的。然而，由於現在圖中存在環，因此信息會繞著圖流動多次。對於某些模型，算法會收斂，而對於其他模型則不會。
為了套用這種方法，我們需要定義一個信息傳遞時間表（message passing schedule）。讓我們假設在任意給定的連結以及任意給定的方向上，每次傳遞一條信息。從一個結點傳送的每條信息替換了之前傳送的任何沿著同一連結的同一方向的信息，並且本身是一個函式，這個函式只與算法的前一步的結點接收到的最近的信息有關。
我們已經看到，只有當結點從所有其他的連結接收到所有其他的信息之後，它才會沿著一條連結傳送信息。由於圖中存在環，因此這就產生了如何初始化信息傳遞算法的問題。為了解決這個問題，我們假設由單位函式給出的初始信息已經在所有方向上通過了每個連結。這樣，每 個結點都處在了傳送信息的位置上。
現在有許多可能的方法來組織信息傳遞時間表。例如，洪水時間表（flooding schedule）在每一步同時向兩個方向沿著每條連結同時傳遞信息，而每次只傳遞一個信息的時間表被稱為連 續時間表（serial schedule）。
根據Kschischnang et al.（2001），對於結點（變數結點或因子結點） aa 和結點 bb ，如果 aa 自從上次向 bb 傳送信息後，從任何其他的連結接收到了任何信息，那么我們說結點 aa 在到結點 bb 的連結上有一個信息掛起（pending）。因此，當一個結點接收到了它的一個連結傳送的信息，就在所有其他的連結上產生了掛起的信息。只有掛起的信息需要被傳送，因為其他的信息僅僅複製了同樣連結上的前一條信息。對於具有樹結構的圖來說，任何只傳送掛起信息的時間表最後會終止於一條在任意方向上沿著任意連結傳送過的信息。此時，沒有掛起信息，並且每個變數接收到的信息給出了精確的邊緣機率分布。然而，在具有環的圖中，算法永遠不會終結，因為總可能存在掛起信息，雖然在實際套用中發現，對於大部分套用，它都會在一個合理的時間內收斂。一旦算法收斂，或者如果未觀測到收斂時算法停止，那么（近似）局部邊緣機率分布可以使用每條連結上的每個變數結點或因子結點最近接收到的輸入信息的乘積進行計算。 +
在一些套用中，循環置信傳播算法會給出很差的結果，而在其他套用中，它被證明非常有效。特別地，對特定類型的誤差修正編碼的最好的解碼算法等價於循環置信傳播算法（Gallager， 1963; Berrou et al.， 1993; McEliece et al.， 1998; MacKay and Neal， 1999; Frey， 1998）。
套用
針對 SIF特徵點匹配錯誤問題：提出一種置信傳播與特徵點形狀特徵相結合去除 SIFT 特徵點匹配錯誤的算法. 該算法分為 4 步：1) 根據每個特徵點的尺度信息、主方向信息以及匹配鄰居特徵點信息確定每個特徵點鄰域視窗的大小和方向，並計算每個特徵點在鄰域視窗內匹配鄰居構成的形狀特徵；
2) 連線每個特徵點與其最近的 3個鄰居特徵點，構成置信傳播網的基本框架；
3)利用每對待確定特徵點對的特徵描述符之間的距離與其形狀特徵之間的距離生成置信傳播網的證據函式，用每對待確定特徵點對與其鄰居之間的空間關係生成置信傳播網的相容函式；
4) 疊代計算每個特徵點的置信度以及傳遞給鄰居的訊息，至整個網路收斂，過最後得到的置信度確定初始匹配特徵點對是否為誤配。用真實拍攝的圖像和牛津幾何視覺組資料庫中的圖像進行仿真實驗，與 RANSAC 算法、GTM 算法以及 BP_SIFT 算法進行了比較, 仿真結果表明, 在召回率、準確率、丟失率和效率上都不錯。
