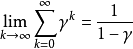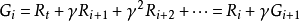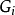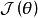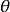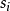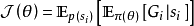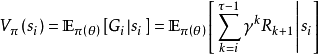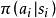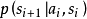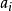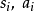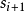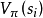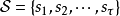歷史
MDP的歷史可以追溯至20世紀50年代動力系統研究中的
最優控制(optimal control)問題,1957年,美國學者Richard Bellman通過離散隨機最優控制模型首次提出了離散時間馬爾可夫決策過程。1960年和1962年,美國學者Ronald A. Howard和David Blackwell提出並完善了求解MDP模型的
動態規劃方法。
進入1980s後,學界對MDP的認識逐漸由“系統最佳化”轉為“學習”。1987年,美國學者Paul Werbos在研究中試圖將MDP和動態規劃與大腦的認識機制相聯繫。1989年,英國學者Chris Watkins首次在強化學習中嘗試使用MDP建模。Watkins (1989)在發表後得到了
機器學習領域的關注,MDP也由此作為
強化學習問題的常見模型而得到套用。
定義
MDP是在環境中模擬智慧型體的隨機性策略(policy)與回報的數學模型,且環境的狀態具有
馬爾可夫性質。
 MDP中智慧型體與環境的互動
MDP中智慧型體與環境的互動互動對象與模型要素
由定義可知,MDP包含一組互動對象,即
智慧型體和環境:
按定義,MDP包含5個模型要素,狀態(state)、動作(action)、策略(policy)、獎勵(reward)和回報(return),其符號與說明在表中給出:
| 名稱 | 符號 | 說明 |
|---|
狀態
狀態空間
| | 狀態是對環境的描述,在智慧型體做出動作後,狀態會發生變化,且演變具有 馬爾可夫性質。MDP所有狀態的集合是狀態空間。狀態空間可以是離散或連續的。 |
動作
動作空間
| | 動作是對智慧型體行為的描述,是智慧型體決策的結果。MDP所有可能動作的集合是動作空間。動作空間可以是離散或連續的。 |
策略 | | MDP的策略是按狀態給出的,動作的條件機率分布,在強化學習的語境下屬於隨機性策略。 |
獎勵 | | 智慧型體給出動作後環境對智慧型體的反饋。是當前時刻狀態、動作和下個時刻狀態的 標量函式。 |
回報
| | 回報是獎勵隨時間步的積累,在引入軌跡的概念後,回報也是軌跡上所有獎勵的總和。 |
在表中建模要素的基礎上,MDP按如下方式進行組織:智慧型體對初始環境
進行感知,按策略
實施動作
,環境受動作影響進入新的狀態
,並反饋給智慧型體一個獎勵
。隨後智慧型體基於
採取新的策略,與環境持續互動。MDP中的獎勵是需要設計的,設計方式通常取決於對應的
強化學習問題。
連續與離散MDP
MDP的指數集(index set)是時間步:
,並按時間步進行演化(evolution)。時間步離散的MDP被稱為離散時間馬爾科夫決策過程(descrete-time MDP),反之則被稱為連續時間馬爾科夫決策過程(continuous-time MDP),二者的關係可類比
連續時間馬爾可夫鏈與離散時間馬爾可夫鏈。
圖模型
MDP可以用圖模型表示,在邏輯上類似於馬爾可夫鏈的轉移圖。MDP的圖模型包含狀態節點和動作節點,狀態到動作的邊由策略定義,動作到狀態的邊由環境動力項(參見求解部分)定義。除初始狀態外,每個狀態都返回一個獎勵。
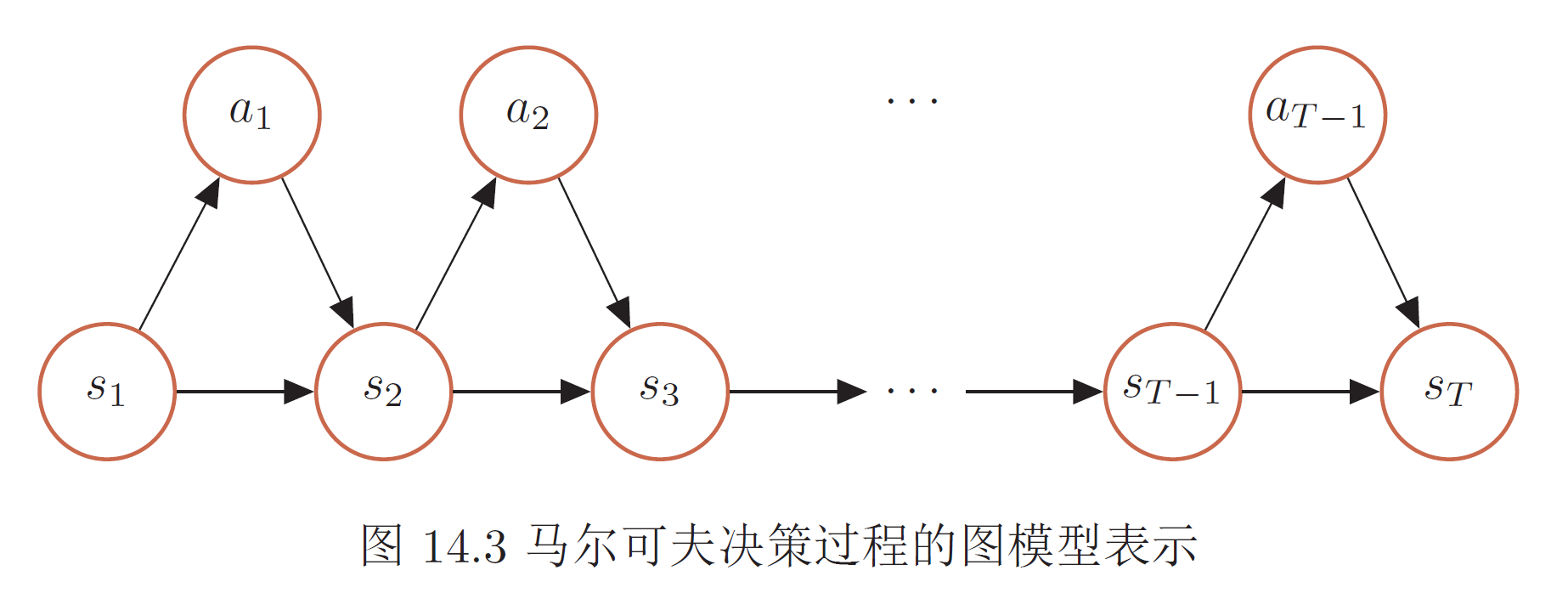 MDP的圖模型表示
MDP的圖模型表示解釋性的例子:多臂賭博機
多臂賭博機問題(multi-armed bandit problem)的設定如下:給定K個不同的賭博機,拉動每個賭博機的拉桿,賭博機會按照一個事先設定的機率掉錢或不掉錢。每個賭博機掉錢的機率不一樣。MDP可以模擬智慧型體選擇賭博機的策略和回報。在該例子中,MDP的要素有如下對應:
“環境”是K個相互獨立的賭博機;“狀態”是“掉錢”和“不掉錢”,其馬爾可夫性質在於每次使用賭博機,返回結果都與先前的使用記錄無關;“動作”是使用賭博機;“策略”是依據前一次操作的賭博機和其返回狀態,選擇下一次使用的賭博機;“獎勵”是一次使用賭博機後掉錢的金額;回報是多次使用賭博機獲得的總收益。
與多臂賭博機類似的例子包括廣告推薦系統和風險投資組合,在MDP建模後,此類問題被視為離散時間步下的紀元式強化學習。
理論與性質
轉移理論
馬爾可夫性質與轉移機率
按定義,MDP具有
馬爾可夫性質,按條件機率關係可表示如下:
即當前時刻的狀態僅與前一時刻的狀態和動作有關,與其他時刻的狀態和動作條件獨立。等式右側的
條件機率被稱為MDP的狀態間的
轉移機率。馬爾可夫性質是所有馬爾可夫模型共有的性質,但相比於
馬爾可夫鏈,MDP的轉移機率加入了智慧型體的動作,其馬爾可夫性質也與動作有關。
MDP的馬爾可夫性質是其被套用於強化學習問題的重要原因,強化學習問題在本質上要求環境的下個狀態與所有的歷史信息,包括狀態、動作和獎勵有關,但在建模時採用馬爾可夫假設可以在對問題進行簡化的同時保留主要關係,此時環境的單步動力學就可以對其未來的狀態進行預測。因此即便一些環境的狀態信號不具有馬爾可夫性,其強化學習問題也可以使用MDP建模。
軌跡
在此基礎上,類比馬爾可夫鏈中的樣本軌道(sample path),可定義MDP的軌跡(trajectory):
即環境由初始狀態
按給定策略
演進至當前狀態
的所有動作、狀態和獎勵的集合。由於MDP的策略和狀態轉移具有隨機性,因此其模擬得到的軌跡是隨機的,且該軌跡出現的機率有如下表示:
一般地,MDP中兩個狀態間的軌跡可以有多條,此時由Chapman-Kolmogorov等式可知,兩個狀態間的n步轉移機率是所有軌跡出現機率的和。
折現
MDP的時間步可以是有限或無限的。時間步有限的MDP存在一個終止狀態(terminal state),該狀態被智慧型體觸發後,MDP的模擬完成了一個紀元(episode)並得到回報。與之對應的,環境中沒有終止狀態的MDP可擁有無限的時間步,其回報也會趨於無窮。
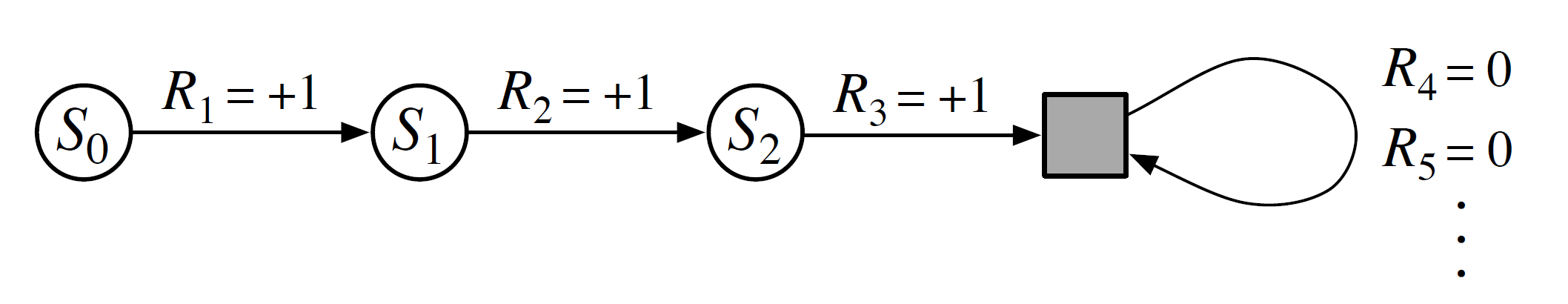 MDP的軌跡與回報計算示例,方形為終止狀態
MDP的軌跡與回報計算示例,方形為終止狀態在對實際問題建模時,除非無限時間步的MDP有收斂行為,否則考慮無限遠處的回報是不適合的,也不利於MDP的求解。為此,可引入折現機制並得到折現回報(discounted return):
式中
為一常數,被稱為折現係數。由幾何級數的極限可知,無限時間步MDP的折現回報是有限的:
因此折現回報在考慮了無窮遠處獎勵的同時,使MDP的求解變得可行。此外為便於計算,折現回報可以表示為遞歸形式:
式中
的下標表示軌跡開始的時間步,對應軌跡
的回報。
值函式
MDP的每組軌跡都對應一個(折現)回報。由於MDP的策略和狀態轉移都是
條件機率,因此在考慮模型的隨機性後,軌跡的折現回報可以由其
數學期望表示,該數學期望被稱為目標函式 :
MDP的軌跡依賴於給定的策略,因此目標函式也是控制策略
的參數的函式:
。例如,若策略由其它機器學習模型,例如神經網路給出,則參數
是權重係數。此外對狀態收斂的無限時間步MDP,其目標函式也可以是其進入平穩分布時單個時間步的獎勵的數學期望。
狀態值函式(state value function)
在MDP模擬的一個紀元中,目標函式與初始狀態
有關,因此按定義,目標函式有可有如下展開:
目標函式中包含初始狀態的條件數學期望被定義為狀態值函式:
,即智慧型體由初始狀態開始,按策略
決定後續動作所得回報的數學期望:
式中的數學期望同時考慮了策略的隨機性和環境的隨機性,為求解值函式,上式可通過折現回報的遞歸形式改寫為
貝爾曼方程(Bellman equation):
上式後兩行中的第一個求和表示對策略的隨機性求數學期望、第二個求和表示對環境,包括狀態和獎勵的隨機性求期望(參見動作值函式)。說明性地,這兩個求和將時間步內所有可能的動作、狀態和獎勵加權求和。由貝爾曼方程的性質可知,給定MDP的策略
、轉移機率
和獎勵
,狀態值函式可以按疊代的方式進行計算。
動作值函式(action value function)
狀態值函式中的條件機率:
表示環境對動作的回響,該項也被稱為環境動力項(environment dynamics)。環境動力項不受智慧型體控制,其數學期望可以定義為動作值函式或Q函式:
,表示智慧型體由給定的狀態
和動作
開始,並按策略
決定後續動作所得到的回報數學期望:
上式為動作值函式的貝爾曼方程,式中關於
的動作值函式包含了
的狀態值函式,聯合上式與動作值函式的貝爾曼方程可以得到二者的相互關係:
式中第二行是另一種形式的動作值函式貝爾曼方程。上式表明,給定策略值函式和動作值函式的貝爾曼方程,可以得到動作值函式的貝爾曼方程。
狀態值函式和動作值函式是一些MDP算法需要使用的,目標函式的變體,其實際意義是對策略的評估。例如在狀態
,若有一個新的動作
使得
,則實施新動作比當前策略
給出的動作要好,因此可通過算法增加新動作所對應的策略
的機率。
算法
在MDP模型建立後,強化學習算法能夠求解一組貫序策略:
,使得目標函式,即智慧型體的折現回報,取全局最大值:
按求解途徑,MDP適用的強化學習算法分為兩類:值函式算法和策略搜尋算法。值函式算法通過疊代策略的值函式求得全局最優;策略搜尋算法則通過搜尋策略空間得到全局最優。
值函式算法
動態規劃(dynamic programming)
作為貝爾曼最最佳化原理(Bellman's principle of Optimality)的推論,有限時間步的MDP至少存在一個全局最優解,且該最優解是確定的(deterministic),可使用動態規劃求得。
使用動態規劃求解的MDP屬於“基於模型的強化學習(model-based reinforcement learning),因為要求狀態值函式和動作值函式的
貝爾曼方程已知,而後者等價於MDP的環境不是”黑箱“,其環境動力項
是已知的。MDP的動態規劃分為策略疊代(policy iteration)和值疊代(value iteration)兩種,其核心思想是
最最佳化原理:最優策略的子策略在一次疊代中也是以該狀態出發的最優策略,因此在疊代中不斷選擇該次疊代的最優子策略能夠收斂至MDP的全局最優。
以策略疊代為例,在對MDP的建模要素初始化後,其每次疊代都使用貝爾曼方程計算狀態值函式以評估策略,並按動作值函式對狀態值函式的貝爾曼方程確定當前狀態下的最優動作和策略:
,疊代在策略的前後變化小於疊代精度時收斂。
隨機模擬
以
蒙特卡羅方法和時序差分學習(temporal-difference learning)為代表的MDP算法屬於“無模型的強化學習(model-free reinforcement learning)”,適用於MDP的環境動力項未知的情形。在MDP的轉移機率未知時,狀態值函式
無法參與最佳化,因此隨機模擬方法通過生成隨機數直接估計動作值函式的真實值並求解MDP。
對給定的初始狀態和動作,蒙特卡羅方法按N次隨機遊走試驗所得回報的平均估計動作值函式:
在動作值函式的隨機遊走收斂後,蒙特卡羅方法按策略疊代尋找最優動作并迭代完成MDP的求解。蒙特卡羅算法在總體上是一個泛用性好但求解效率低下的算法,按確定策略採樣的蒙特卡羅收斂緩慢,在本質上是智慧型體對環境單純的“試錯”。一些引入了探索機制的改進版本,例如ϵ-貪心算法(ϵ-greedy method)也需要採樣整個軌跡後才能評估和改進策略,在求解複雜MDP時會帶來大量計算。
時序差分學習可視為蒙特卡羅方法和動態規劃的結合。在使用採樣方法估計動作值函式時,時序差分學習將採樣改寫為貝爾曼方程的形式,以更高的效率更新動作值函式的取值。求解MDP可用的時序差分學習算法包括SARSA 算法(State Action RewardState Action, SARSA)和Q學習(Q-Learning)算法,二者都利用了MDP的馬爾可夫性質,但前者的改進策略和採樣策略是同一個策略,因此被稱為“同策略(on policy)”算法,而後者採樣與改進分別使用不同策略,因此被稱為“異策略(off policy)”算法。
策略搜尋算法
策略搜尋(policy search)可以在策略空間直接搜尋MDP的最優策略完成求解。策略搜尋算法的常見例子包括REINFORCE算法和演員-評論員算法(Actor-Critic Algorithm)。REINFORCE算法使用隨機梯度上升求解(可微分的)策略函式的參數使得目標函式最大,一些REINFORCE算法的改進版本通過引入基準線加速疊代的收斂。演員-評論員算法是一種結合策略搜尋和時序差分學習的方法。其中“演員(actor)”是指策略函式,即學習一個策略來得到儘量高的回報,“評論員(critic)”是狀態值函式,對當前策略的值函式進行估計,即評估演員的好壞。藉助於值函式,Actor-Critic 算法可以進行單步更新參數。
推廣
約束馬爾可夫決策過程
約束馬爾可夫決策過程(Constrained MDP, CMDP)是對智慧型體施加了額外限制的MDP,在CMDP中,智慧型體不僅要實施策略和獲得回報,還要確保環境狀態的一些指標不超出限制。例如在基於MDP的投資組合問題中,智慧型體除了最大化投資回報,也要求限制投資風險;在交通管理中,智慧型體除了最大化車流量,也要求限制車輛的平均延遲和特定路段的車輛通行種類。
相比於MDP,CMDP中智慧型體的每個動作都對應多個(而非一個)獎勵。此外,由於約束的引入,CMDP不滿足貝爾曼
最最佳化原理,其最優策略是對初始狀態敏感的,因此CMDP無法使用動態規劃求解。離散CMDP的常見解法是
線性規劃(linear programming)。
模糊馬爾可夫決策過程
模糊馬爾可夫決策過程(Fuzzy MDP, FMDP)是使用模糊動態規劃(fuzzy dynamic programming)求解的MDP模型,是MDP的推廣之一。FMDP的求解方法屬於值函式算法,其中策略評估部分與傳統的動態規劃方法相同,但策略改進部分使用了
模糊推理(fuzzy inference),即值函式被用作模糊推理的輸入,策略的改進是模糊推理系統的輸出。
部分可觀察馬爾可夫決策過程
在一些設定中,智慧型體無法完全觀測環境的狀態,此類MDP被稱為部分可觀察馬爾可夫決策過程(Partially Observable MDP,POMDP)。POMDP是一個馬爾可夫決策過程的泛化。POMDP與MDP的馬爾可夫性質相同,但是POMDP框架下智慧型體只能知道部分狀態的觀測值。比如在自動駕駛中,智慧型體只能感知感測器採集的有限的環境信息。與MDP相比,POMDP包含兩個額外的模型要素:智慧型體的觀測機率
和觀測空間
。
套用
 MDP中智慧型體與環境的互動
MDP中智慧型體與環境的互動



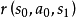


 MDP的圖模型表示
MDP的圖模型表示

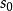
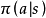

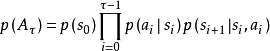
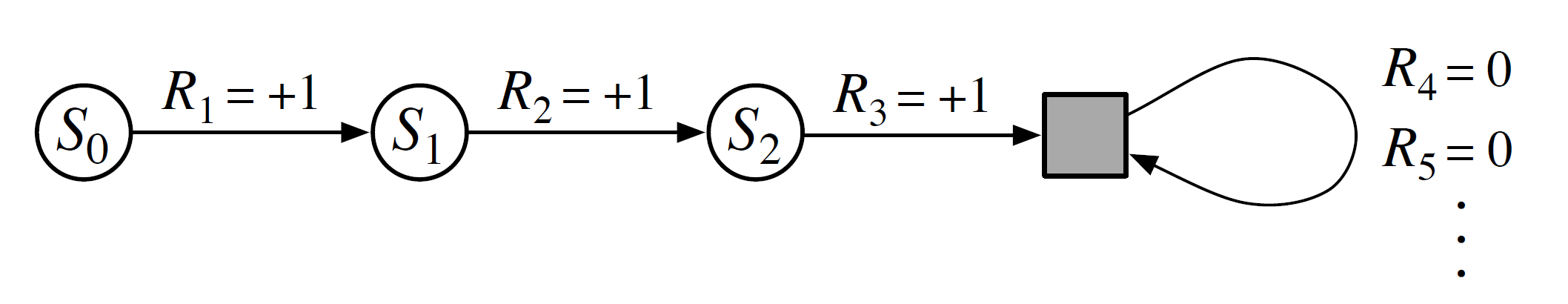 MDP的軌跡與回報計算示例,方形為終止狀態
MDP的軌跡與回報計算示例,方形為終止狀態