分布密度亦稱“機率的分布密度”。設某連續隨機變數落在某區間內的機率為P,△x>0是區間的長度,則P/△x的比值叫做隨機變數在該區間上的“平均機率分布密度”,如果當區間長度△x→0時,比值的極限存在,則這極限叫做隨機變數在點x處的機率分布密度,簡稱分布密度。
基本介紹
- 中文名:分布密度
- 外文名:distribution density
- 所屬領域:數理統計
- 別稱:機率分布密度
- 描述對象:連續性隨機變數
- 相關概念:分布函式、連續性隨機變數等
定義
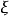



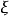

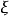
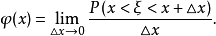
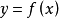
密度函式的性質
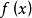
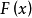
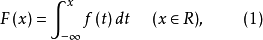
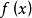
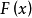
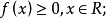
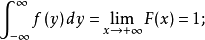
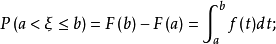
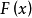
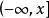


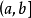


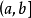

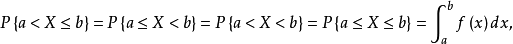




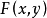
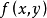

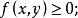
2.

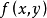



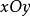


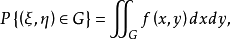



例題解析
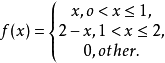
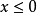

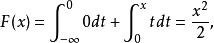



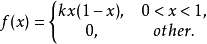
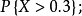

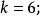
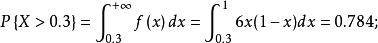
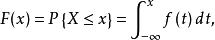



分布密度亦稱“機率的分布密度”。設某連續隨機變數落在某區間內的機率為P,△x>0是區間的長度,則P/△x的比值叫做隨機變數在該區間上的“平均機率分布密度”,如果當區間長度△x→0時,比值的極限存在,則這極限叫做隨機變數在點x處的機率分布密度,簡稱分布密度。
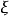



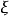

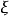
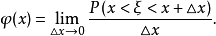
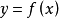
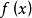
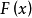
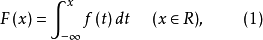
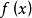
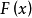
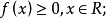
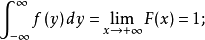
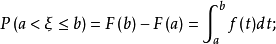
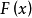
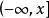


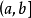


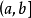
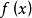

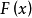
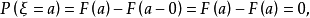
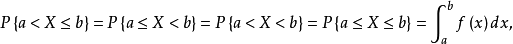




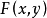
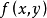

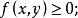

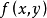



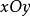


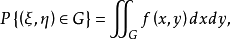



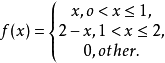
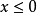

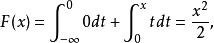



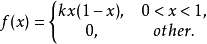
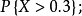

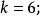
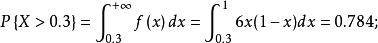
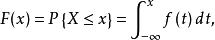


分布密度亦稱“機率的分布密度”。設某連續隨機變數落在某區間內的機率為P,△x>0是區間的長度,則P/△x的比值叫做隨機變數在該區間上的“平均機率分布密度”,...
密度分布,也叫機率密度分布,機率指事件隨機發生的機率,對於均勻分布函式,密度分布等於一段區間(事件的取值範圍)的機率除以該段區間的長度,它的值是非負的,可以很大...
在頻率分布直方圖中,當樣本容量充分放大時,圖中的組距就會充分縮短,這時圖中的階梯折線就會演變成一條光滑的曲線,這條曲線就稱為總體的密度分布曲線。這條曲線排除...
在數學中,連續型隨機變數的機率密度函式(在不至於混淆時可以簡稱為密度函式)是一個描述這個隨機變數的輸出值,在某個確定的取值點附近的可能性的函式。而隨機變數的...
人口密度是單位土地面積上的人口數量。通常使用的計量單位有兩種:人/平方公里;人/公頃。它是衡量一個國家或地區人口分布狀況的重要指標。計算人口密度的土地面積是指...
統計分布(frequency distribution)亦稱“次數(頻數)分布(分配)”。在統計分組的基礎上,將總體中的所有單位按組歸類整理,形成總體單位在各組間的分布。分布在各組中...
若n個相互獨立的隨機變數ξ₁,ξ₂,...,ξn ,均服從標準正態分布(也稱獨立同分布於標準正態分布),則這n個服從標準正態分布的隨機變數的平方和構成一新的...
Logistic分布指當n趨向於無窮大時,從指數分布(exponential distribution)中抽取的容量n的隨機樣本的最大與最小樣本值的平均的極限分布。密度函式為:f(x)=exp[-(x...
在機率論和統計學中,均勻分布也叫矩形分布,它是對稱機率分布,在相同長度間隔的分布機率是等可能的。 均勻分布由兩個參數a和b定義,它們是數軸上的最小值和最大...
大氣密度(atmospherie density)是指單位體積大氣中含有的空氣品質或分子數目。 前者稱質量密度(簡稱密度),單位為千克每立方米;後者稱分子的數密度,單位為m3。...
核密度估計(kernel density estimation)是在機率論中用來估計未知的密度函式,屬於非參數檢驗方法之一,由Rosenblatt (1955)和Emanuel Parzen(1962)提出,又名Parzen窗(...
聯合分布函式(joint distribution function)亦稱多維分布函式,隨機向量的分布函式,以二維情形為例,若(X,Y)是二維隨機向量,x、y是任意兩個實數,則稱二元函式。...
所以在這裡引入一個假設--空間的分布是不均勻的.如此,空間也就有了一個類似於密度的屬性,即空間密度,為了度量空間的密度,引入一個參考系,姑且稱它為絕對空間,那...
對於二維隨機變數(X,Y),可以考慮在其中一個隨機變數取得(可能的)固定值的條件下,另一隨機變數的機率分布,這樣得到的X或Y的機率分布叫做條件機率分布,簡稱條件分布...
如果隨機變數的機率密度函式分布如圖所示,那么它就是拉普拉斯分布,記為x-Laplace(μ,b),其中,μ 是位置參數,b 是尺度參數。如果 μ = 0,那么,正半部分恰好是...
貝塔分布(Beta Distribution) 是一個作為伯努利分布和二項式分布的共軛先驗分布的密度函式,在機器學習和數理統計學中有重要套用。在機率論中,貝塔分布,也稱Β分布,是...
伽瑪分布(Gamma Distribution)是統計學的一種連續機率函式,是機率統計中一種非常重要的分布。“指數分布”和“χ2分布”都是伽馬分布的特例。Gamma分布中的參數α稱...
堆密度是指粉體質量除以該粉體所占容器的體積V求得的密度,亦稱堆密度,即ρb=W/V。填充粉體時,經一定規律振動或輕敲後測得的密度稱振實密度(tapdensity),...
機率指事件隨機發生的機率,對於均勻分布函式,機率密度等於一段區間(事件的取值範圍)的機率除以該段區間的長度,它的值是非負的,可以很大也可以很小。...
正態分布(Normal distribution),也稱“常態分布”,又名高斯分布(Gaussian distribution),最早由A.棣莫弗在求二項分布的漸近公式中得到。C.F.高斯在研究測量誤差時...
公路密度是指每百平方公里或每萬人所擁有的公路總里程數。公路密度是區域公路發展水平的重要標誌, 也是衡量公路作為社會經濟發展中重要基礎設施而滿足交通需求的直觀...
因此,貝葉斯派認為,應該把θ看作是隨機變數。θ的分布函式記為H(θ),θ的密度函式記為h(θ),分別稱為先驗分布函式和先驗密度函式,兩者合稱為先驗分布。...
