統計分布的意義
在統計分組的基礎上,把總體的所有單位數按組歸併排列,形成各組單位數在總體中的分布,稱統計分布。統計分布的實質是,把總體的全部單位按某標誌所分的組進行分配所形成的數列,也可稱為分配數列或分布數列。在每次把某個單位分配到某一組時,人們常常說分配了一次,所以,分配數列又叫次數分布。分配數列有兩個構成要素:一是總體按某標誌所分的組:二是各組對應的單位數——次數。
統計分布形式十分簡單,但在統計研究中卻有著重要的意義。統計分布是統計分析結果的一種重要表現形式,也是統計分析的一種重要方法。它可以表明總體各單位的分布特徵和結構狀況,並有助於我們進一步研究標誌的構成、平均水平及其變動規律。從文字含義看,統計分布理論性強一些,分配數列更通俗一點。以下交叉使用這兩名詞。
統計分布的種類和特徵
分配數列的種類
分配數列有兩個構成要素。即總體按某標誌所分的組和各組對應的次數或頻率。
分配數列的第一個構成要素就是總體按某標誌所分的組。根據分組標誌的不同,分配數列可分為品質分配數列和變數分配數列。按品質標誌分組形成的分配數列叫品質分配數列,簡稱品質數列;按數量標誌分組形成的分配數列叫變數分配數列,簡稱變數數列。變數數列又可以分為單項式數列和組距式數列,組距式數列又可以分為等距數列和不等距數列。它們都是由相應的統計分組形成的。
對品質數列來說,由於用品質標誌來區分事物的各種類型表現得比較明確,因此,品質數列一般比較穩定,能較好地反映總體各單位的分布特徵。但對變數數列來說,因為事物性質的差異是用數量界限來表現的,而數量界限往往會受人們主觀認識的影響,同一數量標誌分組可能會出現多種分布狀態。這就涉及各組頻數和頻率的問題。
頻數和頻率
分配數列的第二個構成要素就是各組對應的單位數——次數,次數也叫頻數,常用
表示。各組單位數占總體單位總數的比重稱頻率,常用
表示。各組的頻率要大於0 且小於1,即
,所有組的頻率總和一定等於1,即
。總體按某標誌所分的組(或以各組的
組中值來代表)與各組對應的頻率所形成的頻率分布也是統計分布,與次數分布的作用是相同的。次數分布和頻率分布都是分配數列。
在變數分配數列中,頻數或頻率表明對應組標誌值的作用程度。頻數或頻率數值越大,表明該組標誌值對總體水平所起的作用也越大;反之,頻數或頻率數值越小,表明該組標誌值對總體水平所起的作用越小。
分配數列中各組的頻數或頻率不能為0,如果某一組的頻數或頻率為0,應刪除這一組。
有時候,為了更簡便地概括總體各單位的分布特徵,還需要編制累計頻數數列和累計頻率數列。累計方法有向上累計和向下累計兩種。
向上累計就是向變數的上限方向累計,是指將各組頻數或頻率由變數值較低的組向變數值較高的組累計,各累計數的意義是各組上限以下的累計頻數或頻率。當我們關註標志值較小的各組分布情況時,可採用向上累計方法。
向下累計就是向變數的下限方向累計,是指將各組頻數或頻率由變數值較高的組向變數值較低的組累計,各累計數的意義是各組下限以上的累計頻數或頻率。當我們關註標志值較大的各組分布情況時,可採用向下累計方法。
分析變數的分布狀況,一般應採用等距數列。此時,各組的頻數或頻率就能很好地反映變數的分布狀況。如果是不等距數列,則應採用各組的次數密度或頻率密度才能正確反映變數的分布狀況。次數密度和頻率密度的計算公式如下:
次數密度=某組次數/該組組距;頻率密度=某組頻率/該組組距
次數分布的特徵
社會經濟現象總體的性質不同,其次數分布的特徵也不同。各種社會經濟現象總體的次數分布,歸納起來主要有鐘型分布、U型分布、J型分布和洛倫茲分布四種類型。
鐘型分布
鐘型分布是常態分配的俗稱,其特徵是“中間高,兩頭低”,即靠近中間的變數值分布的次數多,靠近兩邊的變數值分布的次數少,形如古鐘(見圖1)。
 圖1 鐘型分布
圖1 鐘型分布在社會經濟現象中,鐘型分布多表現為對稱分布。對稱分布的特徵是中間的變數值分布的次數最多,以標誌變數中心為對稱軸。兩側變數值分布的次數隨著與中心變數值距離的增大而漸次減少,並且圍繞中心變數值兩側呈對稱分布。這種分布在統計學中稱為
正態分布。在社會經濟現象中,許多變數的分布近似於常態分配類型。如從業人員的年收入、農作物單產、零件尺寸、學生考試成績、社會財富分布等。常態分配在社會經濟統計學中具有重要意義。這是因為,一方面。社會經濟現象中大部分分布呈近似常態分配;另一方面,常態分配理論是抽樣推斷的基礎。
U型分布
U型分布的特徵與鐘型分布正好相反,靠近中間的變數值分布的次數少,靠近兩端的變數值分布的次數多,形成“兩頭高,中間低”的U字型分布。例如,人口死亡現象按年齡分布便是如此。由於人口總體中幼兒和老年人死亡人數較多,而中年人死亡人數較少,因此,死亡人數按年齡分組便近似地表現為U 型分布,如圖2所示。
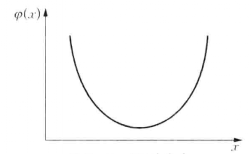 圖2 U型分布
圖2 U型分布J型分布
在社會經濟現象中,一些統計總體分布曲線呈J型,即次數隨著變數值的增加而增加。如農作物產量按土地面積分布、人口數按零售商品銷售額分布、工人數按總產值分布、庫存量按庫存費用分布等,如圖3所示。也有次數隨著變數值的增加而減少的倒J型分布。如企業數按投資額分布、人口數按年齡大小分布等,如圖4所示。
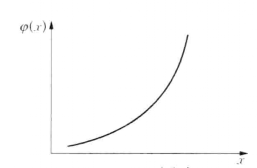 圖3 J型分布
圖3 J型分布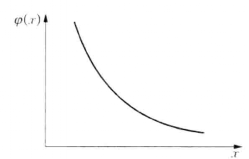 圖4 倒J型分布
圖4 倒J型分布洛倫茲分布
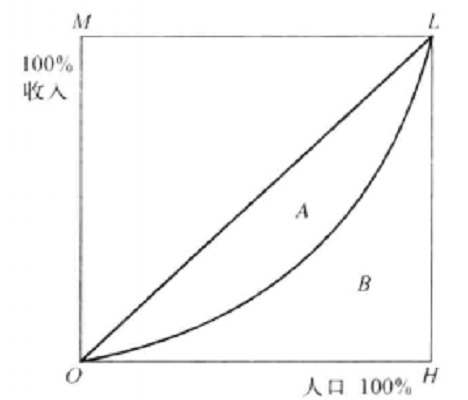
洛倫茲分布曲線是美國統計學家洛倫茲( M.Lorenz)提出來的,專門用以研究社會收入分配的平等問題。
在圖5中。橫軸OH表示人口的累計百分比,縱軸OM表示收入的累計百分比,弧線OL為洛倫茲曲線。洛倫茲曲線的彎曲程度有著重要的意義,它反映了收入分配的不平等程度。彎曲程度越大,收人分配越不平等,反之亦然。
洛倫弦曲線與對角線之間的部分A 叫做“
不平等面積”,直角三角形OHL的面積(A+B)叫做“
完全不平等面積”。不平等面積與完全不平等面積之比,就是
基尼係數,也稱
集中係數:基尼係數=
。
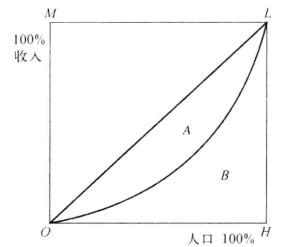 圖5 洛倫茲分布
圖5 洛倫茲分布基尼係數等於1,表示收人分配絕對不平等;基尼係數等於0,表示收人分配絕對平等。基尼係數是衡量,一個國家或地區貧富差距的標準之一。按照聯合國有關組織規定:基尼係數若低於0.2表示收人平均;0.2-0.3表示比較平均;0.3=0.4表示相對合理;0.4-0.5表示收人差距較大;0.5 以上表示收人差距懸殊。通常把0.4作為收人分配差距的“警戒線”。已開發國家的基尼係數在0.26-0.38 之間,我國2013年全國居民收人的基尼係數為0.473。
洛倫茲曲線的拓展可以運用於其他社會經濟現象,研究總體各單位標誌變異狀況——變數分布的均勻性或分布的集中程度,因此,洛倫茲曲線又稱集中曲線。如研究產品市場份額在各企業的集中度以及分析固定資產投資額在各地區的集中度等。
分配數列的編制
(一)將原始資料按其數值大小重新排列
只有把得到的原始資料按其數值大小重新排列順序,才能看出變數分布的集中趨勢和特點,為確定全距、組距和組數作準備。
(二)確定全距
確定
全距前,要檢查數據組兩端有沒有極端值。如果有極端值且個數較少,應考慮將極端值歸入開口組,計算全距前,可去掉極端值。
(三)確定組距和組數
組距=全距/組數,當全距一定時。組距越大,組數就越少;組距越小,組數就越多,在實際套用中。組距一般應採用整數,最好是5或10的整倍數。
(四)確定組限
組限要根據變數的性質來確定。如果變數值相對集中,無特大或特小的極端值時,則採用閉口式:反之,如果有特大或特小的極端值時。則採用開口式,將極端蚊歸入開口組中。
(五)編制變數數列
經過上述四個步驟以後,就可以把總體各單位按變數值的大小分配到各組。計算各組的次數和頻率。



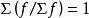
 圖1 鐘型分布
圖1 鐘型分布 圖2 U型分布
圖2 U型分布 圖3 J型分布
圖3 J型分布 圖4 倒J型分布
圖4 倒J型分布
 圖5 洛倫茲分布
圖5 洛倫茲分布