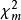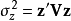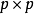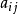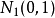以統計學家約翰·威沙特為名的威沙特分布是統計學上的一種半正定矩陣隨機分布。這個分布在多變數分析的共變異矩陣估計上相當重要。
基本介紹
- 中文名:威沙特分布
- 外文名:Wishart distribution
- 分類:人工智慧
定義,常見套用,機率密度函式,特徵函式,理論架構,推論1,推論2,多變數常態分配的估計,分布抽樣,參考條目,
定義
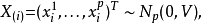
則威沙特分布為 散異矩陣
散異矩陣


的機率分布。

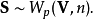
其中正整數 為自由度。有時亦記號為
為自由度。有時亦記號為 。若
。若 且
且 則該分布退化為一自由度為
則該分布退化為一自由度為 的單變數卡方分布。
的單變數卡方分布。





常見套用
威沙特分布常用於多變數的概似比檢定,亦用於隨機矩陣的頻譜理論中。
機率密度函式
威沙特分布具有下述的機率密度函式:
令' 為一
為一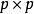 正定對稱隨機變數矩陣。令
正定對稱隨機變數矩陣。令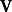 為一特定正定
為一特定正定 矩陣。
矩陣。

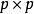
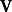

如此,若 ,則
,則 服從於一具自由度n的威沙特分布且有機率度函式
服從於一具自由度n的威沙特分布且有機率度函式



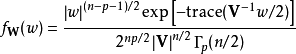
其中 為多變數Gamma分布,其定義為
為多變數Gamma分布,其定義為

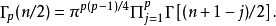
上述定義可推廣至任一實數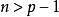
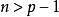
特徵函式
威沙特分布的特徵函式為

也就是說

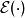
(這裡的 及
及 皆為與
皆為與 維度相同的矩陣。
維度相同的矩陣。 為單位矩陣,而i為-1的平方根)
為單位矩陣,而i為-1的平方根)




理論架構
若 為一自由度為m,共變異矩陣為
為一自由度為m,共變異矩陣為 的威沙特分布,記為—
的威沙特分布,記為—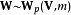 —其中
—其中 為一
為一 的q秩矩陣,則
的q秩矩陣,則


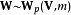



推論1
若 為一非負
為一非負 常數向量,則
常數向量,則



推論2
在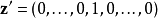 的情形下(亦即第j個元素為1其他為0),推論1可導出
的情形下(亦即第j個元素為1其他為0),推論1可導出
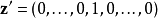
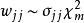
為矩陣的每一個對對角元素的邊際分布。
統計學家George Seber曾論證威沙特分布並非多變數卡方分布,這是因為非對角元素的邊際分布並非卡方分布,Seber傾向於將某某多變數分布此一遣詞用於所有元素的邊際分布皆相同的情形。
多變數常態分配的估計
由於威沙特分布可視為一多變數常態分配其共變異矩陣的最大概似估計量(MLE)的的分布,其衍自MLE的計算可為令人驚喜地簡約而優雅。基於頻譜理論,可將一標量視為一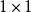 矩陣的跡(trace)。請參考共變異矩陣的估計。
矩陣的跡(trace)。請參考共變異矩陣的估計。
分布抽樣
以下的算法取材自 Smith & Hocking (1972)。一個來自自由度為n及共變異矩陣為 的威沙特分布的
的威沙特分布的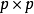 (其中
(其中 )隨機樣本可以如下方式抽樣而得:
)隨機樣本可以如下方式抽樣而得:

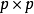

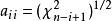
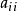
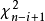
計算 的Cholesky分解。
的Cholesky分解。

計算 。此時,
。此時, 為一
為一 的隨機樣本。
的隨機樣本。



若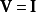 ,則因
,則因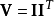 ,可以直接以
,可以直接以 進行抽樣。
進行抽樣。
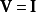
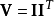

參考條目
- 共變異矩陣的估計
- Hotelling的T平方分布
- 逆威沙特分布