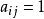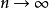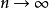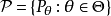統計模型[stochasticmodel；statisticmodel；probabilitymodel]指以機率論為基礎，採用數學統計方法建立的模型。有些過程無法用理論分析方法導出其模型，但可通過試驗測定數據，經過數理統計法求得各變數之間的函式關係，稱為統計模型。常用的數理統計分析方法有最大事後機率估算法、最大似然率辨識法等。常用的統計模型有一般線性模型、廣義線性模型和混合模型。統計模型的意義在對大量隨機事件的規律性做推斷時仍然具有統計性，因而稱為統計推斷。常用的統計模型軟體有SPSS、SAS、Stata、SPLM、Epi-Info、Statistica等。
基本介紹
簡介,數據統計模型,地統計模型,模型的維度,目的,
簡介
統計模型是一組數學模型，它包含了一組關於樣本數據的假設。統計模型通常以相當理想化的形式表示數據生成過程。
統計模型通常由與一個或多個隨機變數以及可能的其他非隨機變數相關的數學方程來指定。因此，統計模型是“理論的形式化表示”。
常用的數理統計分析有最大事後機率估算法，最大似然率辨識法最大事後機率估算法，最大似然率辨識法等。
數據統計模型
多變數統計分析主要用於數據分類和綜合評價。綜合評價是區劃和規劃的基礎。從人類認識的角度來看有精確的和模糊的兩種類型。因為絕大多數地理現象難以用精確的定量關係劃分和表示，因此模糊的模型更為實用，結果也往往更接近實際。模糊評價一般經過四個過程：
(1)評價因子的選擇與簡化；
(2)多因子重要性指標(權重)的確定；
(3)因子內各類別對評價目標的隸屬度確定；
(4)選用某種方法進行多因子綜合。
1.主成分分析
地理問題往往涉及大量相互關聯的自然和社會要素，眾多的要素常常給模型的構造帶來很大困難。為使用戶易於理解和解決現有存儲容量不足的問題，有必要減少某些數據而保留最必要的信息。
主成分分析是通過數理統計分析，求得各要素間線性關係的實質上有意義的表達式，將眾多要素的信息壓縮表達為若干具有代表性的合成變數，這就克服了變數選擇時的冗餘信息，然後選擇信息最豐富的少數因子進行各種聚類分析，構造套用模型。
2.層次分析法(AHP)
Hierarahy Analysis 是T.L.Saaty等在70年代提出和廣泛套用的，是系統分析的數學工具之一，它把人的思維過程層次化、數量化，並用數學方法為分析、決策、預報或控制提供定量的依據。
AHP方法把相互關聯的要素按隸屬關係分為若干層次，請有經驗的專家對各層次各因素的相對重要性給出定量指標，利用數學方法綜合專家意見給出各層次各要素的相對重要性權值，作為綜合分析的基礎。例如要比較n個因素y={y1，y2，…，yn }對目標Z的影響，確定它們在z中的比重，每次取兩個因素yi和yj，用aij表示yi與yj對Z的影響之比，全部比較結果可用矩陣
表示，A叫成對比矩陣，它應滿足：
使上式成立的矩陣稱互反陣，必有
。
3.系統聚類分析
60年代末到70年代初，人們把大量精力集中於發展和套用數字分類法，且將這類方法套用於自然資源、土壤剖面、氣候分類、環境生態等數據，形成“數字分類學”學科。聚類分析已成為標準的分類技術，在許多大型計算機中都存儲了這種分析程式，從GIS資料庫中將點數據傳送到聚類分析程式也不困難。
聚類分析的主要依據是把相似的樣本歸為一類，而把差異大的樣本區分開來。在由m個變數組成為m維的空間中可以用多種方法定義樣本之間的相似性和差異性統計量。
4.判別分析
判別分析就是在已知研究對象分為若干類型(組別)並已經取得各種類型的一批已知樣品的觀測數據基礎上，根據某些準則，建立起儘可能把屬於不同類型的數據區分開來的判別函式，然後用它們來判別未知類型的樣品應該屬於哪一類。根據判別的組數，判別分析可以分為兩組判別分析和多組判別分析;根據判別函式的形式，判別分析可以分為線性判別和非線性判別；根據判別時處理變數的方法不同，判別分析可以分為逐步判別、序貫判別等;根據判別標準的不同，判別分析有距離判別、Fisher判別、Bayes判別等。
判別分析與聚類分析同屬分類問題，所不同的是，判別分析是預先根據理論與實踐確定等級序列的因子標準，再將待分析的地理實體安排到序列的合理位置上的方法，對於諸如水土流失評價、土地適宜性評價等有一定理論根據的分類系統定級問題比較適用。
在地理信息系統中發展了一種多因素模糊評價模型，相當於模糊評判分析。該方法首先根據標準類別參數的指標空間確定各因素各類別對目標的隸屬度，作為判別距離的度量，再結合要素的權重指數，採用適當的模糊算法，計算各地理實體的歸屬等級類別，作為評價的基礎。該方法通過隸屬度表達人們對目標與因素之間關係的模糊性認識，用適當的算法將這種認識量化並反映到結果的分類中，對於地理學中的評價與規劃問題非常有效。
地統計模型
地統計(克里金法)模型包括多個組成部分：檢查數據(分布、趨勢、方向組成和異常值)，計算經驗半變異函式或協方差值，根據經驗值擬合模型，生成克里金方程矩陣以及對其進行求解以為輸出表面中的每個位置獲取預測值及其關聯誤差(不確定性)。
計算經驗半變異函式
與大多數插值法一樣，克里金法基於距離越近的事物就越相似這一基本原則(此處量化為空間自相關)。經驗半變異函式是一種發掘這種關係的方法。在距離上彼此接近的點對應比互相遠離的點對差異小。在經驗半變異函式中可檢查使這種假設成立的範圍。
擬合模型
擬合通過用點定義可提供最佳擬合的模型來實現。也就是說需要找出一條線，使每個點和這條線之間的加權平方差儘可能小。這稱為加權最小二乘擬合。此模型量化數據中的空間自相關。
創建矩陣
進行預測
根據測量值的克里金權重，軟體對包含未知值的位置計算預測值。
模型的維度
如果參數集合統計模型是非參數的
是無限的空間。如果統計模型同時具有有限維和無限維參數，則為半參數。形式上，如果d是維數 和n是樣本的數量，都半參數和非參數模型當
有
。如果
當，那么模型是半參數的；否則，模型是非參數的。
參數模型是迄今為止最常用的統計模型。關於半參數模型和非參數模型，戴維·考克斯爵士曾經說過：“這些模型通常包含更少的結構和分布形式的假設，但通常包含對獨立性的強烈假設。
目的
統計模型是一類特殊的數學模型。統計模型與其他數學模型的區別在於統計模型是非確定性的。因此，在通過數學方程式指定的統計模型中，一些變數不具有特定的值，而是具有機率分布；即一些變數是隨機的。在上面的例子中，ε是一個隨機變數；沒有這個變數，模型將是確定性的。
根據Konishi和Kitagawa的觀點，統計模型有三個目的：
- 預測
- 信息提取
- 隨機結構的描述
