模糊算法

模糊算法屬於智慧型算法，當我們對於系統的模型認識不是很深刻，或者說客觀的原因導致我們無法對系統的控制模型進行深入研究的時候，智慧型算法常常能夠起到不小的作用。常見的模糊算法有均值模糊、高斯模糊等。

基本介紹

• 中文名：模糊算法
• 外文名：Fuzzy algorithm
• 學科：數學
• 套用：圖像處理、信號處理

簡介

實際上模糊算法屬於智慧型算法，智慧型算法也可以叫非模型算法，也就是說，當我們對於系統的模型認識不是很深刻，或者說客觀的原因導致我們無法對系統的控制模型進行深入研究的時候，智慧型算法常常能夠起到不小的作用。這點是方便理解的，如果一個系統的模型可以輕易的獲得，那么就可以根據系統的模型進行模型分析，設計出適合系統模型的控制器。但是現實世界中，可以說所有的系統都是非線性的，是不可預測的。但這並不是說我們就無從建立控制器，因為，大部分的系統在一定的條件和範圍內是可以抽象成為線性系統的。問題的關鍵是，當我們系統設計的範圍超出了線性的範圍，我們又該如何處理。顯然，智慧型算法是一條很不錯的途徑。智慧型算法包含了專家系統、模糊算法、遺傳算法、神經網路算法等。其實這其中的任何一種算法都可以跟PID去做結合，而選擇的關鍵在於，處理的實時性能不能得到滿足。當我們處理器的速度足夠快速時，我們可以選擇更為複雜的、精度更加高的算法。但是，控制器的處理速度限制了我們算法的選擇。當然，成本是限制處理器速度最根本的原因。這個道理很簡單，51單片機和DSP的成本肯定大不相同。專家PID和模糊PID是常用的兩種PID選擇方式。其實，模糊PID適應一般的控制系統是沒有問題。

原理說明

模糊算法其實並不模糊。模糊算法其實也是逐次求精的過程。這裡舉個例子說明。我們設計一個倒立擺系統，假如擺針偏差<5°，我們說它的偏差比較“小”；擺針偏差在5°和10°之間，我們說它的偏差處於“中”的狀態；當擺針偏差>10°的時候，我們說它的偏差有點兒“大”了。對於“小”、“中”、“大”這樣的辭彙來講，他們是精確的表述，可問題是如果擺針偏差是3°呢，那么這是一種什麼樣的狀態呢。我們可以用“很小”來表述它。如果是7°呢，可以說它是“中”偏“小”。那么如果到了80°呢，它的偏差可以說“非常大”。而我們調節的過程實際上就是讓系統的偏差由非常“大”逐漸向非常“小”過度的過程。當然，我們系統這個調節過程是快速穩定的。通過上面的說明，可以認識到，其實對於每一種狀態都可以劃分到大、中、小三個狀態當中去，只不過他們隸屬的程度不太一樣，比如6°隸屬於小的程度可能是0.3，隸屬於中的程度是0.7，隸屬於大的程度是0。這裡實際上是有一個問題的，就是這個隸屬的程度怎么確定？這就要求我們去設計一個隸屬函式。詳細內容可以查閱相關的資料，這裡沒有辦法那么詳細的說明了。那么，知道了隸屬度的問題，就可以根據目前隸屬的程度來控制電機以多大的速度和方向轉動了，當然，最終的控制量肯定要落實在控制電壓上。這點可以很容易的想想，我們控制的目的就是讓倒立擺從隸屬“大”的程度為1的狀態，調節到隸屬“小”的程度為1的狀態。當隸屬大多一些的時候，我們就加快調節的速度，當隸屬小多一些的時候，我們就減慢調節的速度，進行微調。可問題是，大、中、小的狀態是漢字，怎么用數字表示，進而用程式代碼表示呢？其實我們可以給大、中、小三個狀態設定三個數字來表示，比如大表示用3表示，中用2表示，小用1表示。那么我們完全可以用1*0.3+2*0.7+3*0.0=1.7來表示它，當然這個公式也不一定是這樣的，這個公式的設計是系統模糊化和精確化的一個過程，讀者也可參見相關文獻理解。但就1.7這個數字而言，可以說明，目前6°的角度偏差處於小和中之間，但是更偏向於中。我們就可以根據這個數字來調節電機的轉動速度和時間了。當然，這個數字與電機轉速的對應關係，也需要根據實際情況進行設計和調節。

示例

常見的模糊算法比如均值模糊、高斯模糊等其基本的過程都是計算一個像素周邊的的某個領域內，相關像素的某個特徵值的累加和及對應的權重，然後得到結果值。比如均值模糊的各像素的權重是一樣的，而高斯模糊的權重和像素距離中心點的距離成高斯分布。這樣的過程是無法區分出圖像的邊緣等信息的，導致被模糊後的圖像細節嚴重丟失，一種簡單的改進方式就是設定某個閾值，當領域像素和中心點像素的差距大於閾值時，設定其權重很小，甚至為0，這樣對於本身比較平滑的區域，和原始的算法區別不大，而對於像素值變化較為明顯的邊緣地帶，則能夠有效地保留原始信息，這樣就能起到降低噪音的同時保留邊緣的信息。

在實際的處理，小半徑的領域往往處理能力有限，處理的結果不慎理想，而隨著半徑的增加，算法的直接實現耗時成平方關係增長，傳統的最佳化方式由於這個判斷條件的增加，已經無法繼續使用，為了解決速度問題，我們可以採用基於直方圖算法的最佳化，如果能夠統計出領域內的直方圖信息，上述的判斷條件及權重計算就可以簡單的用下述代碼實現：

void Calc(unsigned short *Hist, int Intensity, unsigned char *&Pixel, int Threshold)
{
int K, Low, High, Sum = 0, Weight = 0;
Low = Intensity - Threshold; High = Intensity + Threshold;
if (Low < 0) Low = 0;
if (High > 255) High = 255;
for (K = Low; K <= High; K++)
{
Sum += Hist[K] * K;
Weight += Hist[K];
}
if (Weight != 0) *Pixel = Sum / Weight;
}

在任意半徑局部直方圖類算法在PC中快速實現的框架一文中我們已經實現了任意半徑恆長時間的直方圖信息的獲取，因此算法的執行時間只於上for循環中的循環量有關，也就是取決於Threshold參數，當Threshold取得越大，則最終的效果就越接近標準的模糊算法（上述代碼是接近均值模糊），而在實際有意義的算法套用中而只有Threshold往往要取得較小才有保邊的意義，因此，計算量可以得到適度的控制。

如果要實現選擇性的高斯模糊，則要在for循環中的權重項目中再乘以一個係數，當然這會增加一定的計算量。 我們選擇了一些其他保邊濾波器的測試圖像進行了測試，在效果上通過調整參數能得到相當不錯的效果，舉例如下：

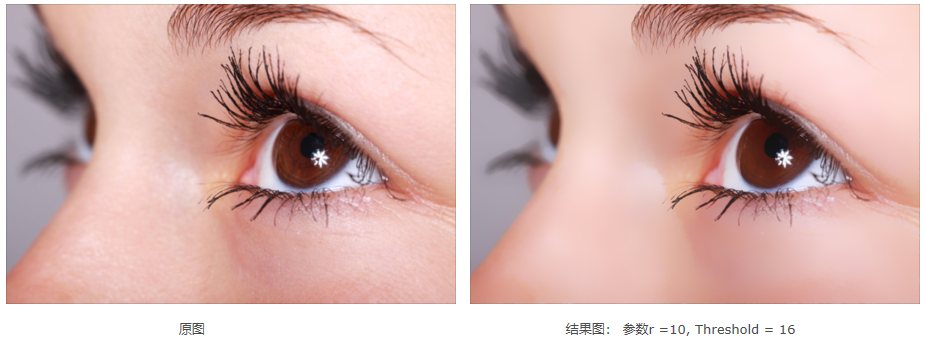圖片處理前後