模糊聚類分析:主要內容,基本方法,基本過程,系統聚類法,逐步聚類法,最優分類,套用

模糊聚類分析是一種採用模糊數學語言對事物按一定的要求進行描述和分類的數學方法。模糊聚類分析一般是指根據研究對象本身的屬性來構造模糊矩陣，並在此基礎上根據一定的隸屬度來確定聚類關係，即用模糊數學的方法把樣本之間的模糊關係定量的確定，從而客觀且準確地進行聚類。聚類就是將數據集分成多個類或簇，使得各個類之間的數據差別應儘可能大，類內之間的數據差別應儘可能小，即為“最小化類間相似性，最大化類內相似性”原則。

基本介紹

中文名：模糊聚類分析
外文名： fuzzy cluster analysis
類型：聚類的分析方法
基本方法：系統聚類法和逐步聚類法
原理：模糊數學

主要內容,基本方法,基本過程,系統聚類法,逐步聚類法,最優分類,套用實例,

主要內容

模糊聚類分析是涉及事物之間的模糊界限時按一定要求對事物進行分類的數學方法。聚類分析是數理統計中的一種多元分析方法，它是用數學方法定量地確定樣本的親疏關係，從而客觀地劃分類型。事物之間的界限，有些是確切的，有些則是模糊的。例人群中的面貌相像程度之間的界限是模糊的，天氣陰、晴之間的界限也是模糊的。當聚類涉及事物之間的模糊界限時，需運用模糊聚類分析方法。模糊聚類分析廣泛套用在氣象預報、地質、農業、林業等方面。通常把被聚類的事物稱為樣本，將被聚類的一組事物稱為樣本集。模糊聚類分析有兩種基本方法：系統聚類法和逐步聚類法。

基本方法

基本過程

編輯

（1）計算樣本或變數間的相似係數，建立模糊相似矩陣；

（2）利用模糊運算對相似矩陣進行一系列的合成改造，生成模糊等價矩陣；

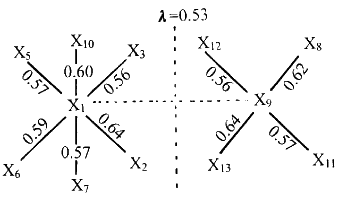
（3）最後根據不同的截取水平λ對模糊等價矩陣進行截取分類

系統聚類法

系統聚類法是基於模糊等價關係的模糊聚類分析法。在經典的聚類分析方法中可用經典等價關係對樣本集X進行聚類。設R是 X上的經典等價關係。對X中的兩個元素x和y，若xRy或(x，y)∈R，則將x和y並為一類，否則x和y不屬於同一類。

套用這種方法,分類的結果與α的取值大小有關。α取值越大,分的類數越多。α小到某一值時,X中的所有樣本歸併為一類。這種方法的優點在於可按實際需要選取α的值，以便得到恰當的分類。

系統聚類法的步驟如下：

①用數字描述樣本的特徵。設被聚類的樣本集為 X={x1，…,xn}。每個樣本均有p種特徵,記作xi=(xi1，…，xip)；i=1，2，…,n；xip表示描述樣本xi的第p個特徵的數。

②規定樣本之間的相似係數rij(0≤rij≤1；i，j=1，…，n)。rij描述樣本xi與xj之間的差異或相似的程度。rij 越接近於1,表明樣本xi與xj之間的差異越小;rij 越接近於0，表明xi與xj之間的差異越大。rij可用主觀評定或集體評分的方法規定，也可用公式計算，如採用夾角餘弦法、最小最大法、算術平均最小法等。因為rii=1(xi與自身沒有差異),rij=rji(xi與xj之間的差異等同於xj與xi之間的差異),所以由rij(i，j=1，…，n)可得X上的模糊相似關係。

一般，R不具備可傳遞性，因而R不一定是 X上的模糊等價關係。

③運用合成運算R=R⋅R（或R=R⋅R等）求出最接近相似關係R的模糊等價關係S=R（或R等）。若R已是模糊等價關係，則取S=R。

④選取適當水平α（0≤α≤1）,得到X 的一種聚類。

逐步聚類法

逐步聚類法是一種基於模糊劃分的模糊聚類分析法。它是預先確定好待分類的樣本應分成幾類，然後按最最佳化原則進行再分類，經多次疊代直到分類比較合理為止。

在分類過程中可認為某個樣本以某一隸屬度隸屬於某一類，又以另一隸屬度隸屬於另一類。這樣，樣本就不是明確地屬於或不屬於某一類。若樣本集有 n個樣本要分成c類，則它的模糊劃分矩陣為此c×n模糊劃分矩陣有下列特性：

①uij∈[0，1]；i=1，…，c；j=1,…，n。

②即每一樣本屬於各類的隸屬度之和為1。

③即每一類模糊子集都不是空集。

最優分類

模糊劃分矩陣有無窮多個，這種模糊劃分矩陣的全體稱為模糊劃分空間。最優分類的標準是樣本與聚類中心的距離平方和最小。

一個樣本是按不同的隸屬度屬於各類的，所以應同時考慮它與每一類的聚類中心的距離。算出最優模糊劃分矩陣後，還必須求得相應的常規劃分。此時可將得到的聚類中心存在計算機中，將樣本重新逐個輸入，去與每個聚類中心進行比較，與哪個聚類中心最接近就屬於哪一類。

這種方法要預先知道分類數，如分類數不合理，就重新計算。這就不如運用基於模糊等價關係的系統聚類法，但可以得到聚類中心，即各類模式樣本，而這往往正是所要求的。因此可用模糊等價關係所得結果作為初始分類，再通過反覆疊代法求得更好的結果。

套用實例

在進行證券交易時，可能會獲得較高的投資收益，但同時也存在著較大的證券投資風險。證券市場是一個風險無時不在的市場，所以投資者應當充分深入的了解證券市場蘊含的各項風險並謹慎行事，從各個方面，綜合考慮投資的利弊，理性投資。隨著股市發張投資手法和證券監管方法的成熟，以及上市公司數量的不斷增多，如何科學合理的進行股票的分析和選擇是每個投資者所要解決的首要問題。

傳統的聚類分析是一種硬劃分，即把每個待辨識的對象嚴格的劃分到某類中，此類劃分的界限是分明的。而實際上大多數對象沒有嚴格的屬性，它們在形態和類屬方面具有“亦此亦彼”的性質。模糊聚類分析可以更好地解決這類問題，模糊聚類分析有多種方法，如傳遞閉包法、最大樹法、編網法等，廣泛套用於許多領域。

最後可以通過綜合指標來選擇股票：

第一類：股票綜合指標較高，發展較好，該類公司發展強勁，潛力比較大，盈利能力較高。該類公司是較好的投資目標，但總體數量不多。
第二類：股票綜合指標相對較低，在幾個方面表現一般。平均意義水平下，每股淨資產較高，說明該公司就有一定資金基礎。主營利潤增長率較高，說明該類公司處於高速成長其，具有較大的發展空間。但該類公司經營有待改善，具有一定的投資價值。
第三類：股票綜合指標非常低，屬於低收益、低成長的“績差股”。各個指標都相對最低，與其他兩類有明顯的差異。這類公司經營穩定性差，發展不順利，不利於投資。該類股票幾乎無投資價值。

模糊聚類分析