基本介紹
定義

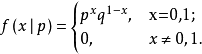
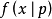


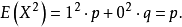


伯努利試驗

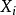







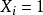



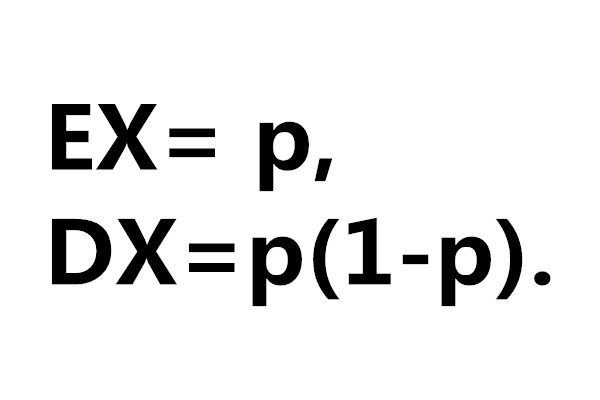

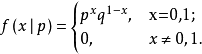
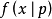


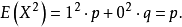



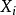







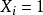



伯努利分布指的是對於隨機變數X有, 參數為p(0<p<1),如果它分別以機率p和1-p取1和0為值。EX= p,DX=p(1-p)。伯努利試驗成功的次數服從伯努利分布,參數p...
伯努利分布(the Bernoulli distribution,又名兩點分布或者0-1分布,是一個離散型機率分布,為紀念瑞士科學家雅各布·伯努利而命名。)若伯努利試驗成功,則伯努利隨機變數...
貝塔分布(Beta Distribution) 是一個作為伯努利分布和二項式分布的共軛先驗分布的密度函式,在機器學習和數理統計學中有重要套用。在機率論中,貝塔分布,也稱Β分布,是...
亦稱伯努利分布、兩點分布。 ...... 亦稱伯努利分布、兩點分布。 [1] 參考資料 1. 鄭家亨,統計大辭典,中國統計出版社,1995年03月第1版,第87頁 V百科往期回顧 ...
先前分布的參數是一種超參數。例如,如果使用beta分布來模擬伯努利分布參數p的分布,則:p是底層系統的參數(伯努利分布),α和β是先前分布(β分布)的參數。...
每一累積量是n倍相對應的伯努利分布。累積量生成函式為g'(t)=n·((p−1)·e+1)。第一累積量為κ1=g'(0)=n·p及κ2=g''(0)=κ1·(1−p)...
1.3聯合分布函式 1.4條件機率與全機率公式 1.5幾類重要的離散型分布 1.5.1伯努利分布 1.5.2二項分布與多項分布 1.5.3幾何分布與負二項分布 1.5.4泊...
第5章 特殊分布 5.1 引言 5.2 伯努利分布與二項分布 5.3 超幾何分布 5.4 泊松分布 5.5 負二項分布 5.6 中心極限定理 5.7 對連續性的修正 5.8 伽瑪分布...
本書介紹實驗物理中涉及的機率和數理統計方面的知識,內容包括機率論初步、隨機變數及其子樣和它們的分布;參數估計(極大似然法、最小二乘法、矩法);假設檢驗;...
第4章 常用分布 183 4.1 伯努利分布 183 4.2 二項分布 186 4.2.1 服從二項分布的隨機變數的 分布律函式 187 4.2.2 二項分布隨機變數是伯努利 隨機變數的和 ...
