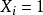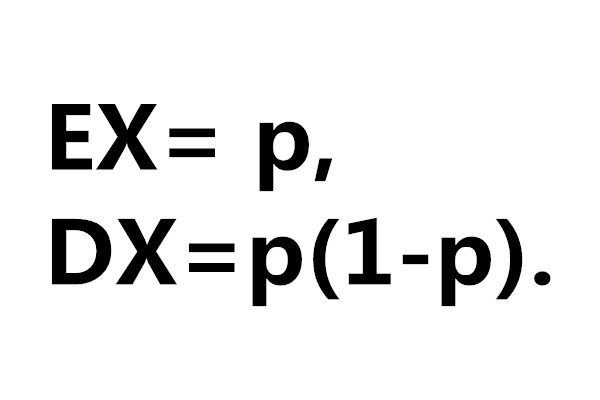伯努利分布

伯努利分布亦稱“零一分布”、“兩點分布”。稱隨機變數X有伯努利分布, 參數為p(0<p<1),如果它分別以機率p和1-p取1和0為值。EX= p,DX=p(1-p)。伯努利試驗成功的次數服從伯努利分布,參數p是試驗成功的機率。伯努利分布是一個離散型機率分布，是N=1時二項分布的特殊情況，為紀念瑞士科學家詹姆斯·伯努利(Jacob Bernoulli 或James Bernoulli)而命名。

基本介紹

• 中文名：伯努利分布
• 外文名：Bernoulli distribution
• 別名：“零一分布”、“兩點分布”
• 特點：試驗結果只有兩個
• 公式：均值EX=p,方差DX=p(1-p)

定義

一個非常簡單的試驗是只有兩個可能結果的試驗，比如正面或反面，成功或失敗，有缺陷或沒有缺陷，病人康復或未康復。為方便起見，記這兩個可能的結果為0和1，下面的定義就是建立在這類試驗基礎之上的。

如果隨機變數X只取0和1兩個值，並且相應的機率為：

則稱隨機變數X服從參數為p的伯努利分布，若令q=1一p，則X的機率函式可寫

為：

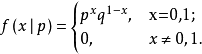
要證明該機率函式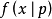 確實是公式所定義的伯努利分布，只要注意到 ，就很容易得證。

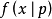
如果X服從參數為p的伯努利分布，則：

並且，

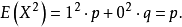
進而，X的矩母函式為：

伯努利試驗

如果無窮隨機變數序列 是獨立同分布(i．i．d．)的，而且每個隨機變數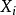 都服從參數為p的伯努利分布，那么隨機變數 就形成參數為p的一系列伯努利試驗。同樣，如果n個隨機變數 獨立同分布，並且都服從參數為p的伯努利分布，則隨機變數 形成參數為p的n重伯努利試驗。

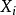
下面舉幾個例子加以說明，假定重複拋擲一枚均勻硬幣，如果在第i次拋擲中出現正面，令 ；如果出現反面，令 ，那么，隨機變數 就形成參數為 的一系列伯努利試驗，同樣，假定由一個特定機器生產的零件中10%是有缺陷的，隨機抽取n個進行觀測，如果第i個零件有缺陷，令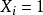 ；如果沒有缺陷，令 ，那么，隨機變數 就形成參數為 的n重伯努利試驗。