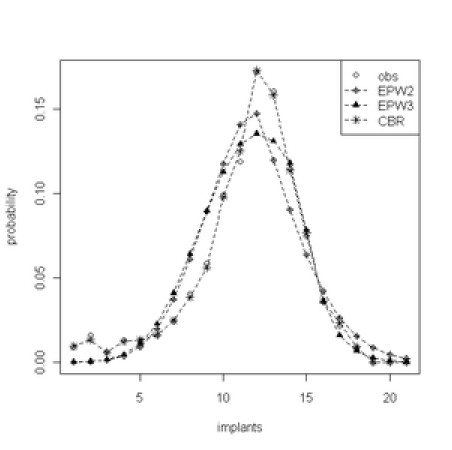
伯努利分布(the Bernoulli distribution,又名兩點分布或者0-1分布,是一個離散型機率分布,為紀念瑞士科學家雅各布·伯努利而命名。)若伯努利試驗成功,則伯努利隨機變數取值為1。若伯努利試驗失敗,則伯努利隨機變數取值為0。記其成功機率為p,則失敗機率為q = 1 − p。其機率質量函式為:
基本介紹
- 中文名:伯努力分布(0-1分布)
- 外文名:the Bernoulli distribution
- 由來:紀念瑞士科學家雅各布·伯努利
- 別稱:兩點分布或者0-1分布
簡介,相關連線,
簡介
伯努力試驗中,被稱為成功的事件,不一定是我們喜歡的結果,而是二結果中,我們較關心或有興趣者。例如,我們可能會記錄共有幾次交通事故,或共有幾人得病等。則每一次交通事故,或每有一人得病,便皆稱為一次成功。
在有些較複雜的隨機試驗中,若我們有興趣的是某特定事件的發生與否,則也會產生伯努力試驗。例如,假設觀察患有某病之病人的存活時間。雖然通常取的值超過兩個但若我們有興趣的為病人是否存活超過5年,則事件便可稱為成功事件,至於其餘集,便稱為失敗事件。如此一來,此試驗就可視為一伯努力試驗了。又如,在某次選舉中,有候選人多位,投票情況當然很複雜。但若我們只關心選民是否會投給某特定候選人,則便化為只有二結果,伯努力試驗又出現了。
由以上討論知,伯努力試驗的例子處處可見。而只有兩個可能結果的試驗,可說是最簡單的試驗了。計算機里採用二進位,以0及1,便可表示出所有的數。在隨機世界裡,也可以只有二結果的伯努力試驗,而繁衍出種種的分布。
伯努力試驗,是因瑞士著名的數學家,機率論創始者之一的JamesBernoulli(1654-1705)而得名。而一隨機變數若滿足,它就是伯努利分布。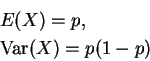
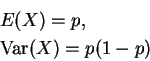
相關連線
伯努力 瑞士 JamesBernoulli 計算機 二進位
伯努力 瑞士 JamesBernoulli 計算機 二進位