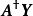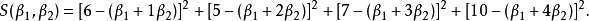最小二乘估計法

最小二乘估計法，又稱最小平方法，是一種數學最佳化技術。它通過最小化誤差的平方和尋找數據的最佳函式匹配。利用最小二乘估計法可以簡便地求得未知的數據，並使得這些求得的數據與實際數據之間誤差的平方和為最小。

基本介紹

• 中文名：最小二乘估計法
• 外文名：Least square estimation
•  領域：數理科學
• 模型：回歸模型
• 套用：回歸分析

簡介

歷史背景

最小二乘法發展於天文學和大地測量學領域，科學家和數學家嘗試為大航海探索時期的海洋航行挑戰提供解決方案。準確描述天體的行為是船艦在大海洋上航行的關鍵，水手不能再依靠陸上目標導航作航行。

這個方法是在十八世紀期間一些進步的集大成：

1）不同觀測值的組合是真實值的最佳估計；多次觀測會減少誤差而不是增加，也許在1722年由Roger Cotes首先闡明。

2）在相同條件下採取的不同觀察結果，與只嘗試記錄一次最精確的觀察結果是對立的。這個方法被稱為平均值方法。托馬斯·馬耶爾（Tobias Mayer）在1750年研究月球的天平動時，特別使用這種方法，而拉普拉斯（Pierre-Simon Laplace）在1788年他的工作成果中以此解釋木星和土星的運動差異。

3）在不同條件下進行的不同觀測值組合。該方法被稱為最小絕對偏差法，出現在Roger Joseph Boscovich在1757年他對地球形體的著名作品，而拉普拉斯在1799年也表示了同樣的問題。

4）評定對誤差達到最小的解決方案標準，拉普拉斯指明了誤差的機率密度的數學形式，並定義了誤差最小化的估計方法。為此，拉普拉斯使用了一雙邊對稱的指數分布，現在稱為拉普拉斯分布作為誤差分布的模型，並將絕對偏差之和作為估計誤差。他認為這是他最簡單的假設，他期待得出算術平均值而成為最佳的估計。可相反地，他的估計是後驗中位數。

最小二乘估計法

1801年，義大利天文學家朱賽普·皮亞齊發現了第一顆小行星穀神星。經過40天的跟蹤觀測後，由於穀神星運行至太陽背後，使得皮亞齊失去了穀神星的位置。隨後全世界的科學家利用皮亞齊的觀測數據開始尋找穀神星，但是根據大多數人計算的結果來尋找穀神星都沒有結果。時年24歲的高斯也計算了穀神星的軌道。奧地利天文學家海因里希·奧伯斯根據高斯計算出來的軌道重新發現了穀神星。

高斯使用的最小二乘法的方法發表於1809年他的著作《天體運動論》中，而法國科學家勒讓德於1806年獨立發現“最小二乘法”，但因不為世人所知而默默無聞。兩人曾為誰最早創立最小二乘法原理髮生爭執。

1829年，高斯提供了最小二乘法的最佳化效果強於其他方法的證明，見馬爾可夫定理。

最小二乘估計法通常歸功於高斯（Carl Friedrich Gauss，1795），但最小二乘估計法是由阿德里安-馬里·勒讓德（Adrien-Marie Legendre）首先發表的。

定義

最小二乘估計法是對過度確定系統，即其中存在比未知數更多的方程組，以回歸分析求得近似解的標準方法。在這整個解決方案中，最小二乘法演算為每一方程式的結果中，將殘差平方和的總和最小化。

最重要的套用是在曲線擬合上。最小平方所涵義的最佳擬合，即殘差（殘差為：觀測值與模型提供的擬合值之間的差距）平方總和的最小化。當問題在自變數有重大不確定性時，那么使用簡易回歸和最小二乘法會發生問題；在這種情況下，須另外考慮變數-誤差-擬合模型所需的方法，而不是最小二乘法。

最小平方問題分為兩種：線性或普通的最小二乘法，和非線性的最小二乘法，取決於在所有未知數中的殘差是否為線性。線性的最小平方問題發生在統計回歸分析中；它有一個封閉形式的解決方案。非線性的問題通常經由疊代細緻化來解決；在每次疊代中，系統由線性近似，因此在這兩種情況下核心演算是相同的。

最小二乘法所得出的多項式，即以擬合曲線的函式來描述自變數與預計應變數的變異數關係。

當觀測值來自指數族且滿足輕度條件時，最小平方估計和最大似然估計是相同的。最小二乘法也能從動差法得出。

回歸分析的最初目的是估計模型的參數以便達到對數據的最佳擬合。在決定一個最佳擬合的不同標準之中，最小二乘估計法是非常優越的。這種估計可以表示為：

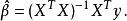
最小二乘法的解

一般線性情況

若含有更多不相關模型變數 ，可如組成線性函式的形式

即線性方程組

通常人們將t_ij記作數據矩陣A，參數b_j記做參數向量b，觀測值y_i記作Y，則線性方程組又可寫成：

即

上述方程運用最小二乘法導出為線性平方差計算的形式為：

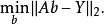
特殊情況——矩陣

的特解為A的廣義逆矩陣與Y的乘積，這同時也是二範數極小的解，其通解為特解加上A的零空間。證明如下：

先將Y拆成A的值域及其正交補兩部分

所以 ，可得

故若且唯若 是 解時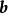， 即為最小二乘解，即 。

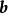
又因為

故 的通解為

因為

所以 又是二範數極小的最小二乘解。

示例

某次實驗得到了四個數據點 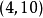： 、 、 、 （圖中紅色的點）。我們希望找出一條和這四個點最匹配的直線 ，即找出在某種“最佳情況”下能夠大致符合如下超定線性方程組的 和 ：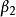

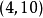
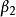
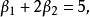
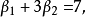
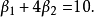
最小二乘估計法採用的手段是儘量使得等號兩邊的方差最小，也就是找出這個函式的最小值：

最小值可以通過對 分別求 和 的偏導數，然後使它們等於零得到。

如此就得到了一個只有兩個未知數的方程組，很容易就可以解出：

也就是說直線 是最佳的。

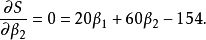
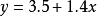
圖1.最小二乘估計法示例

數據點（紅色）、使用最小二乘法求得的最佳解（藍色）、誤差（綠色）。