廣義逆矩陣對於奇異矩陣甚至長方矩陣都存在、具有通常逆矩陣的一些性質、當矩陣非奇異時,它還原到通常的逆矩陣,滿足其3條性質的矩陣叫做廣義逆矩陣。
基本介紹
- 中文名:廣義逆矩陣
- 外文名:generalized inverse matrix
- 定義:是對逆矩陣的推廣
- 例子:奇異矩陣
- 研究領域:數學、計算機
- 最先研究者:E.H.穆爾
簡介
套用領域
歷史

奇異矩陣
定義



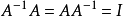

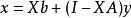


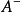




存在條件


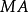

證明







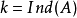



D逆
計算方法







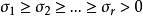
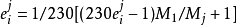
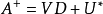
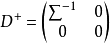



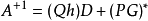



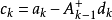


廣義逆矩陣對於奇異矩陣甚至長方矩陣都存在、具有通常逆矩陣的一些性質、當矩陣非奇異時,它還原到通常的逆矩陣,滿足其3條性質的矩陣叫做廣義逆矩陣。




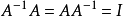

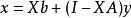


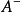






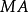








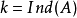










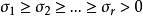
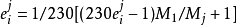
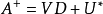
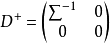



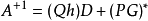



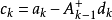

廣義逆矩陣對於奇異矩陣甚至長方矩陣都存在、具有通常逆矩陣的一些性質、當矩陣非奇異時,它還原到通常的逆矩陣,滿足其3條性質的矩陣叫做廣義逆矩陣。...
《廣義逆矩陣的理論與方法》,是作者是陳永林。2005年南京師大出版社出版...... 《廣義逆矩陣的理論與方法》除了介紹廣義逆矩陣的一些基本知識外,主要反映在前述關於...
穆爾-彭羅斯廣義逆矩陣(Moore-Penrose generalized inverse matrix)是逆矩陣概念的推廣,彭羅斯(R.Penrose)於1995年證明了對任一m×n階矩陣A,都存在惟一的n×m階...
穆爾一彭羅斯廣義逆矩陣(Moore-Penrose gen-eralized inverse matrix)一種廣義逆矩陣.設A是sXn復矩陣,如果nX:復矩陣G滿足: 則G稱為A的穆爾一彭羅斯廣義逆矩陣. ...
7.1 廣義逆矩陣及其分類7.2 廣義逆矩陣Aˉ7.3 廣義逆矩陣A+7.4* 廣義逆矩陣的通式7.5 廣義逆矩陣的套用習題7第8章 特徵值的估計及廣義特徵值...
本書系統、概括地論述了工程中常用的矩陣理論和方法,主要包括:線性空間與線性變換、酉空間和酉變換、矩陣的分解、範數及其套用、矩陣分析、矩陣函式、廣義逆矩陣、...
本書適合工科類研究生作為矩陣論教材.全書共分六章(約50學時),主要講解矩陣的基本理論與方法, 包括線性空間與線性變換,常見的矩陣分解,廣義逆矩陣,矩陣分析,矩陣...
最後三章是廣義逆矩陣的幾何基礎和矩陣處理,非負矩陣的基本性質和復矩陣偶在相抵下的標準形。《線性代數與矩陣論》的特點是充分發揮矩陣技巧在矩陣論和線性空間理論...
全書共分為五章,分別介紹了線性空間與線性變換、λ-矩陣與Jordan標準形、矩陣分析及矩陣函式、矩陣微分方程、廣義逆矩陣等內容。各章生面配有一定數量的習題,並在...
矩陣範數,矩陣微積分及其套用,廣義逆矩陣及其套用,幾類特殊矩陣與特殊積(如非負矩陣與正矩陣、循環矩陣與素矩陣、隨機矩陣和雙隨機矩陣、單調矩陣、M矩陣與H矩陣、...
7.2 矩陣的QR分解7.3 矩陣的滿秩分解7.4 矩陣的奇異值分解習題7第八章 廣義逆矩陣8.1 廣義逆矩陣及其分類8.2 廣義逆矩陣A-...
矩陣的逆和偽逆是數學領域中線性代數關於矩陣的名詞。...... 偽逆矩陣是逆矩陣的廣義形式。 對於矩陣A,如果存在一個矩陣B,使得AB=BA=E,其中E為與A,B同維數的...
而矩陣論又可分為矩陣方程論、矩陣分解論和廣義逆矩陣論等矩陣的現代理論。矩陣的套用是多方面的,不僅在數學領域裡,而且在力學、物理、科技等方面都十分廣泛的套用...
系統地介紹矩陣的基本理論、方法和某些套用,主要包括線性代數基礎、矩陣分解、範數理論及其套用、矩陣分析、特徵值的估計、廣義逆矩陣、非負矩陣和Kroneker積與矩陣...
主要內容為線性空間與線性映射、內積空間與等距變換、矩陣的相似標準形、Hermite二次型、範數理論、矩陣函式及廣義逆矩陣等,每章有一定數量的習題,部分習題給出了...
考慮到矩陣理論的完整性、系統性,又能反映最新進展,同時為滿足某些專業多學時教學的需要,本書的下篇安排有: 第6章介紹廣義逆矩陣及其套用;第7章介紹矩陣的因子...
1.7 逆矩陣1.8 廣義逆矩陣1.9 Moore-Penrose逆矩陣1.10 Hadamard積與Kronecker本章小結習題第2章 特殊矩陣2.1 對稱矩陣、Hermitian 矩陣與循環矩陣2.2 基本矩陣...
3.3連線矩陣 3.4變換的一般約束――恆功率變換 3.5變換的廣義逆矩陣 3.6電機的解耦變換 3.7慣用解耦變換問題 第四章 控制電機 4.1旋轉變壓器 4.2自整角機 4.3...
4.3.2正規矩陣的譜分解4.4矩陣的奇異值分解4.5廣義逆矩陣*4.6廣義逆矩陣與線性方程組的求解4.6.1A(1)與線性方程組的解4.6.2A(1,4)與線性方程組的極小範數解...
曾遠榮,數學家。長期從事泛函分析研究,是我國開展這一領域研究的先驅者之一,在廣義逆等研究領域成就卓著。...
於1955年,當他還是學生之時,彭羅斯重新發明了廣義逆矩陣(又稱作摩爾—彭若斯廣義逆(Moore-Penrose inverse)。參見羅傑·彭羅斯 "A Generalized Inverse for Matrices...
