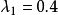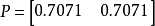主成分分析法:簡介,基本思想,主要目的,分析步驟,MATLAB實現,套用分析,套用

主成分分析也稱主分量分析，通過主成分分析法可以起到降低維度的作用，把多指標合成為少數幾個相互無關的綜合指標（即主成分），其中每個主成分都能夠反映原始變數的絕大部分信息，而且所含信息互不重複。這種方法在引進多方面變數的同時將複雜因素歸結為幾個主成分，使問題簡單化，同時得到更加科學有效的數據信息。

在實際問題研究中，為了全面、系統地分析問題，我們必須考慮眾多影響因素。這些涉及的因素一般稱為指標，在多元統計分析中也稱為變數。因為每個變數都在不同程度上反映了所研究問題的某些信息，並且指標之間彼此有一定的相關性，因而所得的統計數據反映的信息在一定程度上有重疊。主要方法有特徵值分解，SVD，NMF等。

基本介紹

中文名：主成分分析法
外文名：principal component analysis
簡稱：PCA
實質：數據降維方法

簡介,基本思想,主要目的,分析步驟,MATLAB實現,套用分析,套用,因子旋轉,問題,

簡介

principal component analysis(PCA)　主成分分析法是一種數學變換的方法, 它把給定的一組相關變數通過線性變換轉成另一組不相關的變數，這些新的變數按照方差依次遞減的順序排列。在數學變換中保持變數的總方差不變，使第一變數具有最大的方差，稱為第一主成分，第二變數的方差次大，並且和第一變數不相關，稱為第二主成分。依次類推，I個變數就有I個主成分。

其中Li為p維正交化向量（Li*Li=1），Zi之間互不相關且按照方差由大到小排列，則稱Zi為X的第I個主成分。設X的協方差矩陣為Σ，則Σ必為半正定對稱矩陣，求特徵值λi（按從大到小排序）及其特徵向量，可以證明，λi所對應的正交化特徵向量，即為第I個主成分Zi所對應的係數向量Li，而Zi的方差貢獻率定義為λi/Σλj,通常要求提取的主成分的數量k滿足Σλk/Σλj>0.85。

進行主成分分析後，還可以根據需要進一步利用K-L變換（霍特林變換）對原數據進行投影變換，達到降維的目的。

基本思想

PCA的基本原理就是將一個矩陣中的樣本數據投影到一個新的空間中去。對於一個矩陣來說，將其對角化即產生特徵根及特徵向量的過程，也是將其在標準正交基上投影的過程，而特徵值對應的即為該特徵向量方向上的投影長度，因此該方向上攜帶的原有數據的信息越多。

主要目的

是希望用較少的變數去解釋原來資料中的大部分變數，將我們手中許多相關性很高的變數轉化成彼此相互獨立或不相關的變數。通常是選出比原始變數個數少，能解釋大部分資料中變數的幾個新變數，即所謂主成分，並用以解釋資料的綜合性指標。由此可見，主成分分析實際上是一種降維方法。

分析步驟

將原始數據按行排列組成矩陣X
對X進行數據標準化，使其均值變為零
求X的協方差矩陣C
將特徵向量按特徵值由大到小排列，取前k個按行組成矩陣P
通過計算Y = PX，得到降維後數據Y
用下式計算每個特徵根的貢獻率Vi;Vi=xi/(x1+x2+........)
根據特徵根及其特徵向量解釋主成分物理意義。

舉例來說，二維平面有5個點，可以用2*5的矩陣X來表示：

對X進行歸一化，使X每一行減去其對應的均值，得到：

求X的協方差矩陣：

求解C的特徵值，利用線性代數知識或是MATLAB中eig函式可以得到：

對應的特徵向量分別是：

將原數據降為一維，選擇最大的特徵值對應的特徵向量，因此P為：

降維後的數據：

MATLAB實現

MATLAB中自帶了進行主成分分析的函式，在命令行中輸入help pca可以查到該函式的以下幾種用法：

coeff = pca(X)

coeff = pca(X,Name,Value)

[coeff,score,latent] = pca(___)

[coeff,score,latent,tsquared] = pca(___)

[coeff,score,latent,tsquared,explained,mu] = pca(___)

其中，coeff為為X所對應的協方差矩陣的特徵值向量，latent為特徵值組成的向量，score是原X矩陣在主成分空間的表示，tsquared表示霍特林T方統計值。

對應上面的例子，MATLAB代碼為：

X = [1 2 3 4 5;1 3 2 5 4];X=X-3;[coeff, ~, latent] = pca(X');[~,i] = max(latent);P = coeff(:,i);Y = P'*X;

輸出得到的結果相同。

套用分析

套用

在社會調查中，對於同一個變數，研究者往往用多個不同的問題來測量一個人的意見。這些不同的問題構成了所謂的測度項，它們代表一個變數的不同方面。主成分分析法被用來對這些變數進行降維處理，使它們“濃縮”為一個變數，稱為因子。

在用主成分分析法進行因子求解時，我們最多可以得到與測度項個數一樣多的因子。如果保留所有的因子，就起不到降維的目的了。但是我們知道因子的大小排列，我們可以對它們進行舍取。哪有那么多小的因子需要捨棄呢？在一般的行為研究中，我們常常用到的判斷方法有兩個：特徵根大於1法與碎石坡法。

因為因子中的信息可以用特徵根來表示，所以我們有特徵根大於1這個規則。如果一個因子的特徵根大於1就保留，否則拋棄。這個規則，雖然簡單易用，卻只是一個經驗法則(rule of thumb)，沒有明確的統計檢驗。不幸的是，統計檢驗的方法在實際中並不比這個經驗法則更有效(Gorsuch, 1983)。所以這個經驗法則至今仍是最常用的法則。作為一個經驗法則，它不總是正確的。它會高估或者低估實際的因子個數。它的適用範圍是20-40個的測度項，每個理論因子對應3-5個測度項，並且樣本量是大的 ( 3100)。

碎石坡法是一種看圖方法。如果我們以因子的次序為X軸、以特徵根大小為Y軸，我們可以把特徵根隨因子的變化畫在一個坐標上，因子特徵根呈下降趨勢。這個趨勢線的頭部快速下降，而尾部則變得平坦。從尾部開始逆向對尾部畫一條回歸線，遠高於回歸線的點代表主要的因子，回歸線兩旁的點代表次要因子。但是碎石坡法往往高估因子的個數。這種方法相對於第一種方法更不可靠，所以在實際研究中一般不用。

拋棄小因子、保留大因子之後，降維的目的就達到了。

因子旋轉

在對社會調查數據進行分析時，除了把相關的問題綜合成因子並保留大的因子，研究者往往還需要對因子與測度項之間的關係進行檢驗，以確保每一個主要的因子（主成分）對應於一組意義相關的測度項。為了更清楚的展現因子與測度項之間的關係，研究者需要進行因子旋轉。常見的旋轉方法是VARIMAX旋轉。旋轉之後，如果一個測度項與對應的因子的相關度很高（>0.5)就被認為是可以接受的。如果一個測度項與一個不對應的因子的相關度過高（>0.4），則是不可接受的，這樣的測度項可能需要修改或淘汰。

用主成分分析法得到因子，並用因子旋轉分析測度項與因子關係的過程往往被稱為探索性因子分析。

在探索性因子分析被接受之後，研究者可以對這些因子之間的關係進行進一步測試，比如用結構方程分析來做假設檢驗。

問題

問題的提出主成分分析是一種降維的方法,便於分析問題,在諸多領域中都有廣泛的套用。但有些教科書與論文使用主成分分析時,出現了一些錯誤與不足,不能解決實際問題。如一些多元統計分析的教材中,用協方差矩陣的主成分分析出現了如下錯誤與不足:①沒有明確和判斷該數據降維的條件是否成立。②主成分係數的平方和不為1。③沒有明確和判斷所用數據是否適合作單獨的主成分分析。④選取的主成分對原始變數沒有代表性。以下從相關性等理論與結果上依次解決上述問題,並給出相應建議。
數據在行為與心理研究中,常常要求分析某種身份的人的行為特徵,如本例中的小學生的日常行為特徵,從而根據這些特徵引導小學生向更積極的行為態度發展。這裡用文獻[1]的數據見表1,其來自某課題組的調查結果。課題組對北方某國小480名5～6年級學生的日常行為進行調查,共調查了11項指標如下:S1～對老師提問的反應、S2～對班級事務的關心、S3～自習課上的表現、S4～對家庭作業的態度、S5～關心同學的程度、S6～對待勞動的態度、S7～學習上的特殊興趣、S8～對待體育鍛鍊的態度、S9～在娛樂上的偏好、S10～解決問題的思考方式、S11～對未來的打算

主成分分析法和層次分析法異同

1.基於相關性分析的指標篩選原理

兩個指標之間的相關係數，反映了兩個指標之間的相關性。相關係數越大，兩個指標反映的信息相關性就越高。而為了使評價指標體系簡潔有效，就需要避免指標反映信息重複。通過計算同一準則層中各個評價指標之間的相關係數，刪除相關係數較大的指標，避免了評價指標所反映的信息重複。通過相關性分析，簡化了指標體系，保證了指標體系的簡潔有效。

2.基於主成分分析的指標篩選原理

（1）因子載荷的原理

通過對剩餘多個指標進行主成分分析，得到每個指標的因子載荷。因子載荷的絕對值小於等於1，而絕對值越是趨向於1，指標對評價結果越重要。

（2）基於主成分分析的指標篩選原理

因子載荷反映指標對評價結果的影響程度，因子載荷絕對值越大表示指標對評價結果越重要，越應該保留；反之，越應該刪除。1通過對相關性分析篩選後的指標進行主成分分析，得到每個指標的因子載荷，從而刪除因子載荷小的指標，保證篩選出重要的指標。

3.相關性分析和主成分分析相同點

一是，基於相關性分析的指標篩選和基於主成分分析的指標篩選，均是在準則層內進行指標的篩選處理，準則層之間不進行篩選。這種做法的原因是，通過人為地劃分不同準則層，反映評價事物不同層面的狀況，避免誤刪反應信息不同的重要指標。

二是，基於相關性分析的指標篩選和基於主成分分析的指標篩選的思路，均是篩選出少量具有代表性的指標。

4.相關性分析和主成分分析不同點

一是，兩次篩選的目的不同：基於相關性分析的指標篩選的目的是刪除反應信息冗餘的評價指標。基於主成分分析的指標篩選的目的是刪除對評價結果影響較小的評價指標。

二是，兩次篩選的作用不同：基於相關性分析的指標篩選的作用是保證蹄選出的評價指標體系簡潔明快。基於主成分分析的指標簡選的目的是篩選出重要的指標。

主成分分析法