正交化是指將線性無關向量系轉化為正交系的過程。設{xn}是內積空間H中有限個或可列個線性無關的向量,則必定有H中的規範正交系{en}使得對每個正整數n(當{xn}只含有m個向量,要求n≤m),xn是e1,e2,…,en的線性組合。
基本介紹
- 中文名:正交化
- 外文名:orthogonalization
- 學科:數學、物理
- 方法:施密特正交化方法
簡介
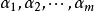
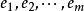
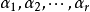
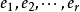
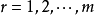
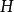
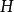
證明
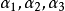
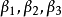
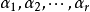




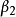
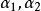


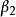

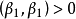
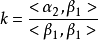
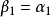


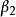
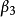
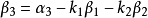
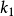

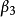

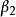

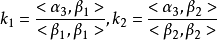


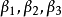



正交化是指將線性無關向量系轉化為正交系的過程。設{xn}是內積空間H中有限個或可列個線性無關的向量,則必定有H中的規範正交系{en}使得對每個正整數n(當{xn}只含有m個向量,要求n≤m),xn是e1,e2,…,en的線性組合。
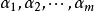
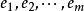
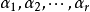
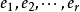
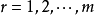
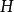
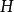
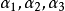
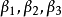
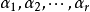




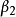
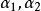


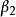

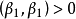
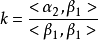
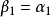


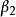
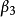
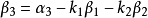
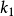

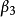

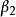

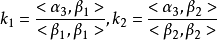


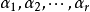
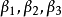


正交化是指將線性無關向量系轉化為正交系的過程。設{xn}是內積空間H中有限個或可列個線性無關的向量,則必定有H中的規範正交系{en}使得對每個正整數n(當{xn...
施密特正交化(Schmidt orthogonalization)是將一組線性無關的向量變成一單位正交向量組的方法。...
“正交性”是從幾何中借來的術語。如果兩條直線相交成直角,他們就是正交的。用向量術語來說,這兩條直線互不依賴。沿著某一條直線移動,該直線投影到另一條直線上...
施密特正交化(Schmidt orthogonalization)是求歐氏空間正交基的一種方法。從歐氏空間任意線性無關的向量組α1,α2,……,αm出發,求得正交向量組β1,β2,……,...
在定義了內積之後,我們可以對這組基矢進行更嚴格的要求——正交;事實上通過施密特正交化(Schmidt orthogonalization),我們也總能將一組線性獨立的基矢變成正交的。...
在左矢量空間中仿照右矢量空間定義內積,之後通過施密特正交化,就可以得到正交左矢。中文名 正交左矢 外文名 orthogonal base bras 目錄 1 引入 2 性質 正交左矢...
正交試驗設計(Orthogonal experimental design)是研究多因素多水平的又一種設計方法,它是根據正交性從全面試驗中挑選出部分有代表性的點進行試驗,這些有代表性的點...
介紹 吉文斯正交化方法(Givens orthogonalizationmethod)解線性最小二乘問題的常用方法之一其基本步驟與豪斯霍爾德方法一樣,只是在約化過程中使用吉文斯變換(參見“豪斯...
正交系是互相正交的函式系的簡稱,用於微分方程、積分方程、計算方法等數學領域。...... 可用格雷姆一休密特(Gram—Schmidt)正交化程式構造出標準正交向量組,在內積空間...
把線性無關向量系進行正交化的過程,稱為格拉姆-施密特正交化過程。...... 這種把線性無關向量系進行正交化的過程,稱為格拉姆-施密特正交化過程。 [1] ...
線上性代數和泛函分析中,投影是從向量空間映射到自身的一種線性變換,是日常生活中“平行投影”概念的形式化和一般化。同現實中陽光將事物投影到地面上一樣,投影...
回歸正交設計,是指試驗方案的結構矩陣具有正交性的回歸設計。是在正交設計基礎上發展起來的,可建立方程,選擇最佳的方案。其突出優點是用很少的處理組合得出完全實施...
在定義了內積之後,我們可以對這組基右矢進行更嚴格的要求——正交;事實上通過施密特正交化(Schmidt orthogonalization),我們也總能將一組線性獨立的基矢變成正交的。...
正交試驗設計,是指研究多因素多水平的一種試驗設計方法。根據正交性從全面試驗中挑選出部分有代表性的點進行試驗,這些有代表性的點具備均勻分散,齊整可比的特點。...
正交是線性代數的概念,是垂直這一直觀概念的推廣。作為一個形容詞,只有在一個確定的內積空間中才有意義。若內積空間中兩向量的內積為0,則稱它們是正交的。如果...
線上性代數中,一個內積空間的正交基(orthogonal basis)是元素兩兩正交的基。稱基中的元素為基向量。假若,一個正交基的基向量的模長都是單位長度1,則稱這正交基...
正交向量組是一組非零的兩兩正交(即內積為0)的向量構成的向量組。幾何向量的概念線上性代數中經由抽象化,得到更一般的向量概念。此處向量定義為向量空間的元素,...
如果AAT=E(E為單位矩陣,AT表示“矩陣A的轉置矩陣”)或ATA=E,則n階實矩陣A稱為正交矩陣。正交矩陣是實數特殊化的酉矩陣,因此總是屬於正規矩陣。儘管我們在這裡...
正交信號的自相關函式具有理想衝擊函式的形式,互相關函式為零。然而由能量守恆原理知道,這樣的理想信號是不存在的。因此,需要對發射信號進行最佳化設計,使得信號的自...
Schimidt正交化是無關向量組的一種證明過程。...... 很容易證明這樣得到的向量組,而且用數學歸納法很容易證明是一個正交向量組。我們把這一過程稱為Schimidt正交化,...
正交多項式系(system of orthogonal polynomials)是正交函式系的一種。...... 按施密特方法關於ρ(x)正交化,適當規定最高次項的係數,即可得到在(a,b)上關於ρ(x...
正交多項式是由多項式構成的正交函式系的通稱。...... 對於同一權函式的正交多項式系雖然很多,但是首項係數為 1的正交多項式系或首項係數為正的規範正交多項式系卻...
“正交向量”是一個數學術語,指點積為零的兩個或多個向量。幾何向量的概念線上性代數中經由抽象化,得到更一般的向量概念。此處向量定義為向量空間的元素,要注意...
《複雜材料的電子結構方法:原子軌道正交化線性組合》是2015年出版的圖書,ISBN是978-7-312-03623-1。...
