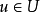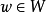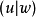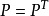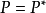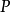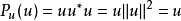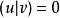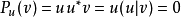基本介紹
- 中文名:正交投影
- 外文名:Orthogonal projection
- 又稱:平行投影
- 釋義:投影線垂直於投影面的投影
- 學科:數學
定義,簡單例子,基本性質,正交投影,例子,斜投影,在賦范向量空間上的投影,參見,
定義
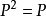
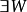
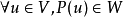
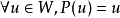
簡單例子
在現實生活中,陽光在地面上留下各種影子。這就是投影變換最直白的例子。可以理想化地假設陽光都是沿著同一個方向(比如說垂直於地面的角度)照射而來,大地是嚴格的平面,那么,對於任意一個物體(比如說一隻正在飛行的鳥),它的位置可以用向量(x,y,z)來表示,而這隻鳥在陽光下對應著一個影子,也就是(x,y,0)。這樣的一個變換就是一個投影變換。它將三維空間中的向量(x,y,z)到映射到向量(x,y,0)。這是在x-y平面上的投影。這個變換可以用矩陣表示為
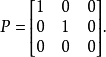
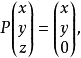
另外,
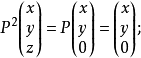
基本性質
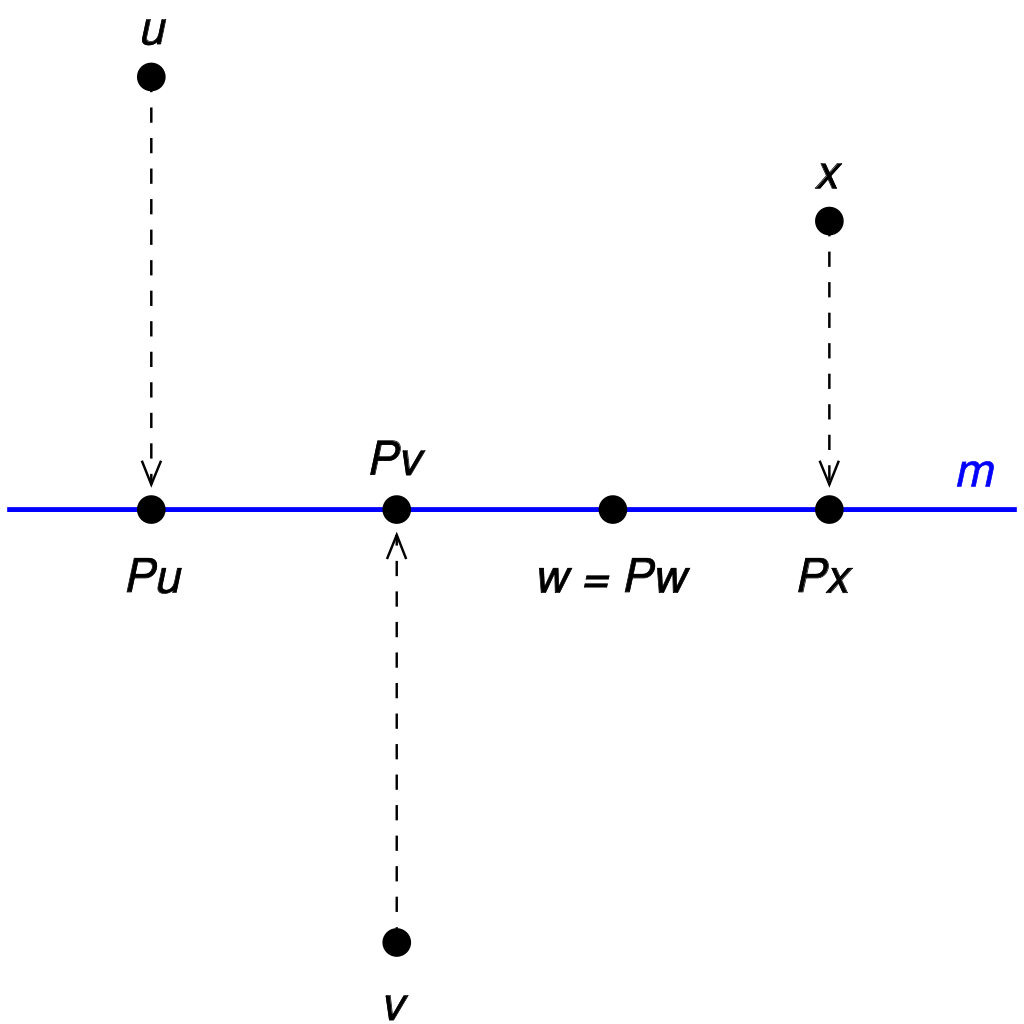
這裡假定投影所在的向量空間V是有限維的(因此不需要考慮如投影的連續性之類的問題)。假設子空間U與W分別為P的像空間與零空間(也叫做核)。那么按照定義,有如下的基本性質: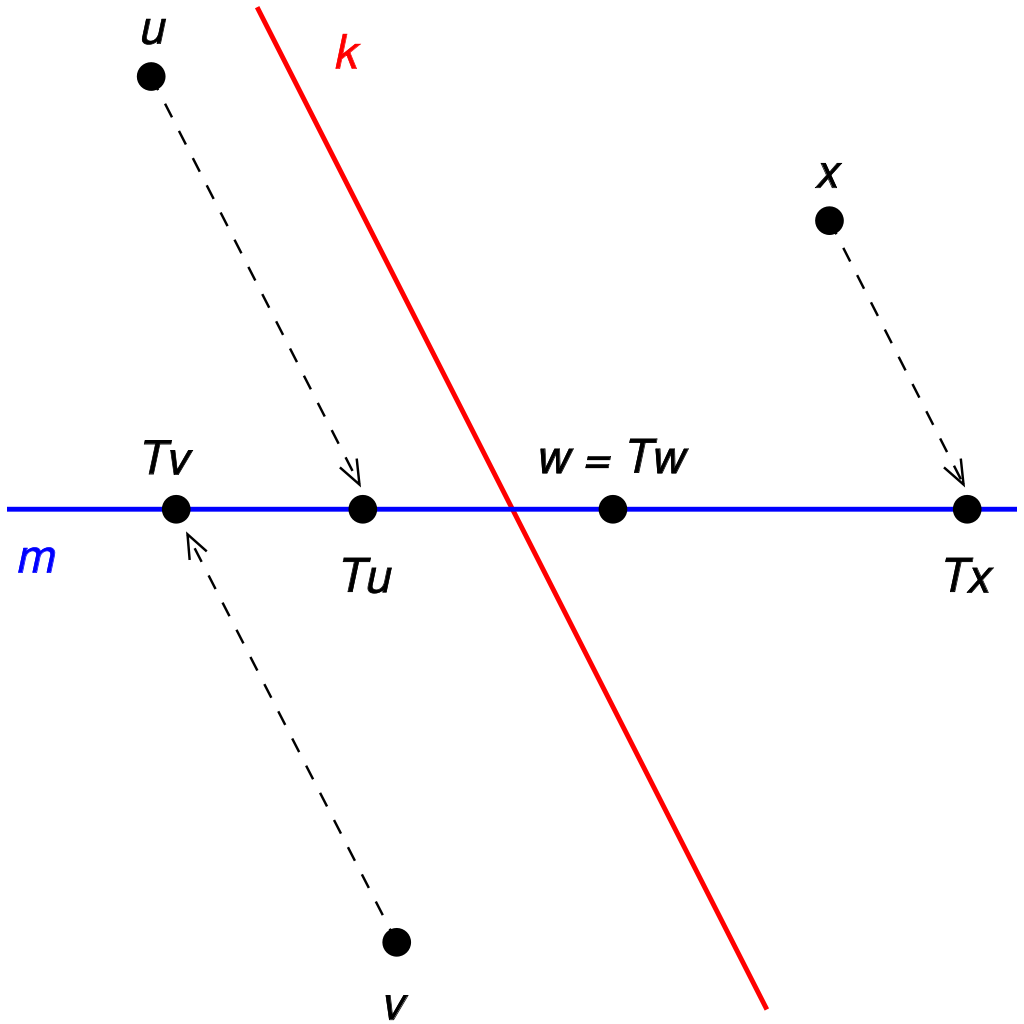 圖1.變換T是沿著k方向到直線m上的投影
圖1.變換T是沿著k方向到直線m上的投影
 圖1.變換T是沿著k方向到直線m上的投影
圖1.變換T是沿著k方向到直線m上的投影P在像空間U上是恆等變換: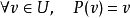 。
。
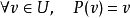
整個向量空間可以分解成子空間U與W的直和: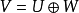 。也就是說,空間裡的每一個向量
。也就是說,空間裡的每一個向量 ,都可以以唯一的方式寫成兩個向量
,都可以以唯一的方式寫成兩個向量 與
與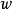 的和:
的和: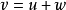 ,並且滿足
,並且滿足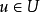 、
、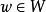 。事實上,每一個向量
。事實上,每一個向量 都可以寫成
都可以寫成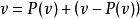 。
。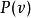 顯然在像空間中,而另一方面
顯然在像空間中,而另一方面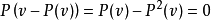 ,所以
,所以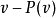 在零空間中。
在零空間中。
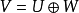


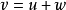
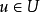
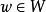

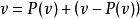
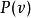
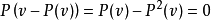
用抽象代數的術語來說,投影P是冪等的線性變換。因此它的極小多項式是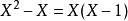 。因式分解後可以看到,這個多項式只有相異的單根(沒有多重根),因此P是可對角化矩陣。極小多項式也顯示出了投影的特性:像空間與零空間分別是是對應於特徵值1和0的特徵空間,並給出了整個空間的一個直和分解。
。因式分解後可以看到,這個多項式只有相異的單根(沒有多重根),因此P是可對角化矩陣。極小多項式也顯示出了投影的特性:像空間與零空間分別是是對應於特徵值1和0的特徵空間,並給出了整個空間的一個直和分解。
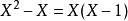
正如日常生活中陽光沿著一定的方向將影子投射到地面上,一般的投影變換也可以稱為是沿著W到U上的投影。由於向量空間分解成直和的方式一般不是唯一的(陽光可以順著不同的方向照射),給定一個子空間V(地面),一般的說有很多到V的投影(沿不同的W)。
正交投影
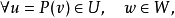
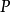
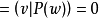
例子
正交投影的最簡單的情況是到(過原點)直線上的正交投影。如果u是這條直線的單位方向向量,則投影給出為
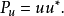
這個公式可以推廣至到在任意維的子空間上的正交投影。設u1,…,uk是子空間U的一組正交基,並設A為一個n×k的矩陣,它的列向量是u1,…,uk。那么投影:
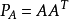
正交條件也可以去除。如果u1,…,uk是(不必須正交)基,而A是有這些向量作為列的矩陣,則投影是
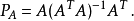
所有這些公式對於複數內積空間也成立,假如用共軛轉置替代轉置。
斜投影
術語斜投影有時用來提及非正交投影。這些投影也用來在二維繪圖中表示空間圖形(參見斜投影),儘管不如正交投影常用。
斜投影用它們的值域和零空間來定義。有給定值域和零空間的投影的矩陣表示的公式可如下這樣找到。設向量u1, …,uk形成了投影的值域的基,並把這些向量組合到n×k矩陣A中。值域和零空間是互補空間,所以零空間有維度n−k。它推出零空間的正交補有維度k。設v1, …,vk形成這個投影的零空間的正交補的基,並把這些向量組合到矩陣B中。則投影定義為
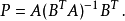
這個表達式一般化上面給出的正交投影公式。
在賦范向量空間上的投影
假定X是巴拿赫空間,給定的X的直和分解成補子空間仍指定一個投影,反之亦然。如果X是直和X=U⊕V,則定義自P(u+v)=u的運算元仍是有值域U和核V的投影。明顯的也P=P。反過來說,如果P是在X上的投影,就是說P=P,則很容易驗證(I−P)=(I−P)。換句話說,(I−P)也是投影。關係I=P+(I−P)蘊涵了X是直和Ran(P)⊕Ran(I−P)。
但是相對於有限維情況,投影一般不必須是連續的。如果X的子空間U在規範拓撲下不閉合,則到U上的投影是不連續的。換句話說,連續投影P的值域一定是閉合子空間。進一步的,連續投影(事實上,一般的連續線性運算元)的核是閉合的。所以連續投影P把X分解成兩個互補的閉合子空間:X=Ran(P)⊕Ker(P)=Ran(P)⊕Ran(I−P)。
反命題在有額外假定條件下也成立。假設U是X的閉合子空間。如果存在一個閉合子空間V使得X=U⊕V,則有值域U和核V的投影P是連續的。這是從閉合圖定理推出的。假定xn→x而Pxn→y。需要證明Px=y。因為U是閉合的且{Pxn}⊂U,y位於U中,就是說Py=y。還有xn−Pxn=(I−P)xn→x−y。因為V是閉合的且{(I−P)xn}⊂V,我們有了x−y∈V,就是說P(x−y)=Px−Py=Px−y=0,這證明了這個斷言。