簡介
透視投影是用
中心投影法將形體投射到投影面上,從而獲得的一種較為接近視覺效果的單面投影圖。它具有消失感、距離感、相同大小的形體呈現出有規律的變化等一系列的透視特性,能逼真地反映形體的
空間形象。
透視投影符合人們心理習慣,即離視點近的物體大,離視點遠的物體小,遠到極點即為消失,成為
滅點。它的
視景體類似於一個頂部和底部都被切除掉的棱椎,也就是
稜台。這個投影通常用於動畫、視覺仿真以及其它許多具有真實性反映的方面。
現實生活中的景物,由於觀察距離及方位的不同在視覺上會引起不同的反映,這種現象就是透視現象。研究透視現象並使之能在平面上用線來表現其規律,使畫面可正確地表現出物體遠近之間的層次關係,使觀察者獲得立體、有深度的空間感覺,就必須研究透視變換的規律。
投影
投影變換是在世界坐標系中建立的,而計算機螢幕所顯示的圖形是在給定視點和視線方向下的二維螢幕投影。所以投影變換是整個圖形變換的關鍵。根據投影中心與投影平面之間距離的不同,投影可分為透視投影和正射投影。
透視投影類似於人對客觀世界的觀察方式,它的特點是距離視點近的物體比較大,而距離遠的物體相對比較小,這種投影方式的視景空間可以被認為是一個稜台。它廣泛套用於三維地形模擬、飛行穿越仿真、步行穿越仿真等模擬人眼視覺效果的研究領域。
正射投影是物體直接映射到螢幕上。正射投影實質上是透視投影的一種特例,即視點在無窮遠或視點由一個點變為一個面。它適用於某地的頂視效果圖、地形暈渲圖或需要觀察模型某一個側面不帶有形變的景觀等。
透視圖繪製方法
利用計算機繪製或顯示物體的透視圖,常採用圖形變換的矩陣方法。一般是按下列兩種方法來獲得物體透視圖。按透視變換的矩陣方法作透視圖時,畫面必須是空間透射變換的二重面,即透射軸平面,否則得到的將不是透視投影,而只是一個經各種變換後得到的二維圖形。
1、把物體平移到適當位置後,進行射影變換,然後繞坐標軸旋轉,最後向某一坐標面進行正投影。
2、把物體平移到適當位置後,進行繞坐標軸的旋轉變換,然後施以射影變換,最後向某一坐標面進行正投影。
然而,不論採用哪種方法,得到的圖形常會出現較大的變形。其原因,除開採用這些方法時難於較好地選定物體、畫面和視點的相對位置外,更主要的是運用這些方法有時不能得到真正的透視圖。
空間透射相關定義
空間透射
空間透射(Stereohomology)——從空間場k1到k2的廣義射影變換T,若變換存在一個不動點的軌跡平面(稱之為界面),且對任意點P∈k1及其對應點P'∈k2存在一固定點S(稱之為透射中心)與PP'共線。則稱T是從k1到k2的空間透射變換。
空間透視
空間透視(Stereoperspective)——是透射中心S在界面c上且皆為固有元素的滿秩空間透射變換。
中心投影
中心投影(CentralProjection)——是透射中心S為可及點(亦即固有點),界面c為可及平面(亦即固有平面)的降秩空間透射變換。
平行投影
平行投影(ParallelProjection)——是透射中心S為不可及點(非固有點)而界面c為可及(固有)平面的降秩空間透射變換。
平移變換
平移變換(TranslationTransformation)——是透射中心S及界面c皆非固有元素的滿秩空間透射變換。
中心輻射相似變換
中心輻射相似變換(CentralRadiationSimilarTransformation)——是透射中心S為固有點而界面c為非固有平面的滿秩空間透射。
透視投影矩陣變換
投影變換是圖形變換的關鍵內容,是聯繫三維空間物體與二維螢幕圖形的橋樑。在三維圖形顯示中,一般採用透視投影變換,其變換矩陣也有多種形式。
過渡坐標系
透視投影的視線(投影線)是從視點(觀察點)出發,視線是不平行的。透視投影按主滅點個數分為一點透視、二點透視和三點透視,任何一束不平行於投影平面的透視投影將匯聚成一點,稱之為滅點,在坐標軸上的滅點稱為主滅點。
三維圖形顯示採用的投影一般為一點透視投影,在簡單一點透視投影變換中,由於投影平面取成坐標系中的一個坐標平面,因此用一個坐標系即可表示透視投影變換,如圖。
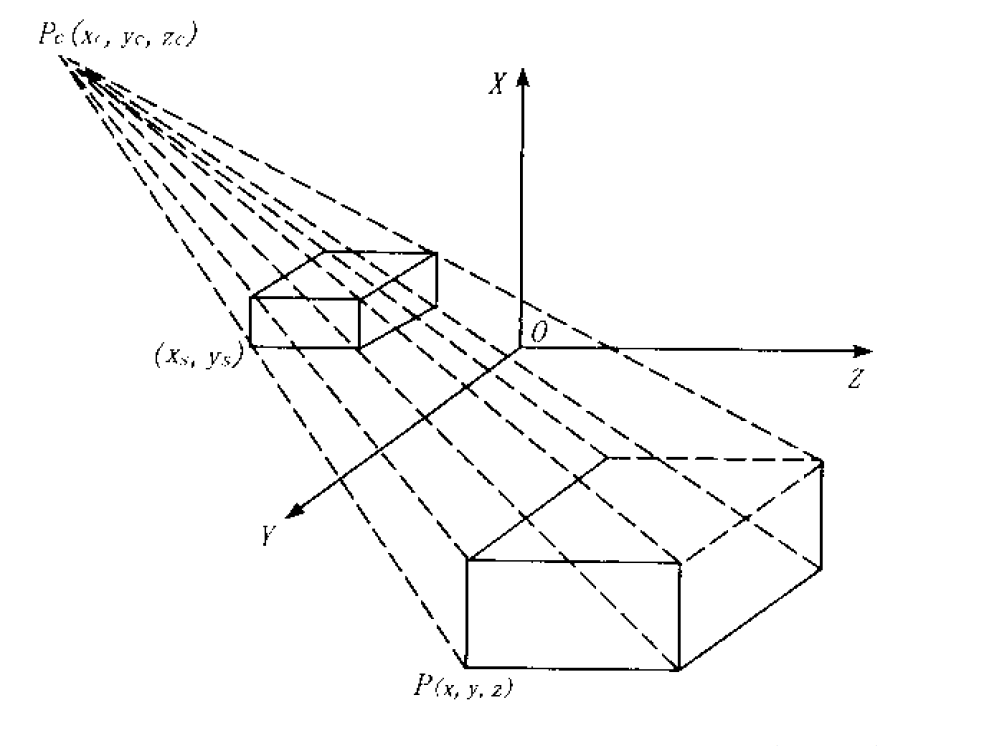 簡單的一點透視投影
簡單的一點透視投影在透視投影中往往要求物體不動,讓視點在以形體為中心的球面上變化來觀察形體各個方向上的形象,解決的辦法是引入一個過渡坐標系,即視點坐標系。
視點坐標系是左手三維直角坐標系,與一般物體所在的世界坐標系不同,是以人眼為坐標原點,坐標軸遵循左手法則,即左手大拇指指向Z軸的正方向,與之垂直的4個手指指向X軸的正方向,四指彎曲成90°的方向是Y軸的正方向。
實現矩陣變換
引入了過渡坐標系後,透視投影變換可看作是兩個基本變換,即世界坐標繫到視點坐標系的變換和視點坐標繫到螢幕坐標系的變換。變換矩陣有如下五步:
(1)將世界坐標系的原點平移到視點
(2)令平移後的新坐標軸繞X'軸旋轉90°,則形體上的點是順轉90°。
(3)將新坐標系繞y'順時針轉θ角,此時θ角大於180°,形體頂點逆轉θ角。
(4)再令新坐標系繞x'順時針轉φ角,形體頂點逆轉φ。
(5)右手坐標系變成左手坐標系,Z軸反向。
 簡單的一點透視投影
簡單的一點透視投影
 簡單的一點透視投影
簡單的一點透視投影