基本介紹
性質
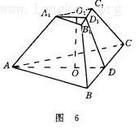
稜台組成
體積







表面積















稜台是幾何學中研究的一類多面體,指一個稜錐被平行於它的底面的一個平面所截後,截面與底面之間的幾何形體。截面也稱為稜台的上底面,原來稜錐的底面稱為下底面...
四稜台(Square frustum)一種特殊台梯形體(好比正方形與長方形),即底面與頂面均為正方形或長方形,側面都是等腰梯形,四條棱的延長線能夠交匯於一點的一種台體...
稜錐的底面和平行於底面的一個截面間的部分,叫做稜台。截面間是四邊形的稜台叫做四稜台。由正稜錐截得且截面間是正方形的稜台叫做正四稜台。兩個平行的面分別...
斜稜台(oblique prismoid)一種特殊的台體.指由斜稜錐截得的稜台...... 斜稜台(oblique prismoid)一種特殊的台體.指由斜稜錐截得的稜台.斜稜台(oblique prismoid...
由正稜錐截得的稜台叫做正稜台。...... (2)正稜台的兩底面以及平行於底面的截面是相似正多邊形;(3)正稜台的兩底面中心連線、相應的邊心距和斜高組成一個直角...
在正圓錐體、正稜錐體、正圓台或正稜台等空間幾何體的側面多邊形中,底邊上的高線即為斜高。...
上、下面平行且為長方形(特殊情況有兩個相對的面是正方形,即四稜台),四個側面都是梯形由此圍成的立體圖形叫梯形體...
當稜台為正稜台時,簡化公式為:相當於底面、頂面均為正方型,即a=b,c=d;v=1/2(a^2+c^2)h-1/6(a-c)(a-c)h=1/3h(a^2+c^2+2a﹒c)...
稜錐的底面和平行於底面的一個截面間的部分,叫做稜台。由三稜錐,四稜錐,五稜錐……截得的稜台,分別叫做三稜台,四稜台,五稜台……...
稜台 S1和S2——上、下底面積 h——高 圓柱 r——底面半徑 h——高 S=2πrh+2πr² 圓錐 r——底半徑 h---高 l——母線 S=πrl+πr...
圖3 稜台的中截面 【例】把一個稜台的高三等分,過各個分點作平行於底面的截面,已知稜台的兩個底面面積分別為q和Q,求各個截面的面積 [4] 。...
正稜台體積推導 v=1/2a﹒b﹒h (用三稜柱立式來算也是該結果) 像這種非標準狀態恰恰是現有公式根本無法計算的(只要不立起來算)柱...
就如同錐台,雙錐台也可以依據所截的是雙圓錐還是雙稜錐,可分為雙圓台與雙稜台。 雙錐台可以視為雙錐體截去二個極點,因此也可以稱為截角雙錐體或截頂雙錐體。...
