雙錐台

在幾何學中，雙錐台又稱雙平截頭體（英語：Bifrustum）是指三個相似的平形的平面圖形如同錐體或柱體構造其側面使圖形封閉，通常中間的面最大，上下二個面等大，但較中間面小，或是指一個雙錐體被兩個平行平面，一個在赤道面上方、一個在赤道面下方所截後，位於兩個平行平面之間的立體，或是可以看做是二個錐台以相同的底面相皆後所形成的幾何圖形，第三種者定義較廣，包含凹雙錐台，第二種者只包含凸雙錐台，但也有上下不對稱的雙錐台。就如同錐台，雙錐台也可以依據所截的是雙圓錐還是雙稜錐，可分為雙圓台與雙稜台。

雙錐台可以視為雙錐體截去二個極點，因此也可以稱為截角雙錐體或截頂雙錐體。

雙錐台的對偶多面體是雙角錐柱。

雙錐台也是一種分子構形。

基本介紹

• 中文名：雙錐台
• 外文名：Bifrustum
• 領域：幾何學

雙錐台的形狀

一般來說雙錐台具有2n個梯形，2n個多邊形，並且對偶為雙角錐柱。

圖1.雙三角錐台:6個梯形、2三角形，對偶為雙三角錐柱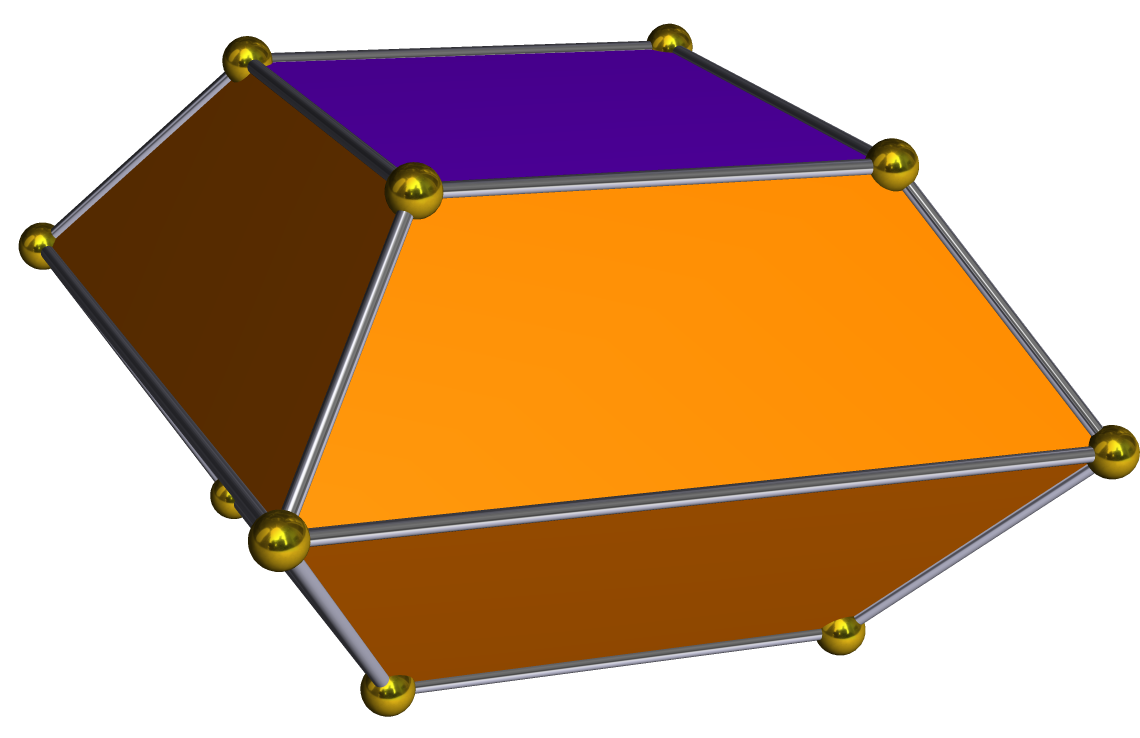

圖2.雙四角錐台:8個梯形、2正方形，對偶為雙四角錐柱

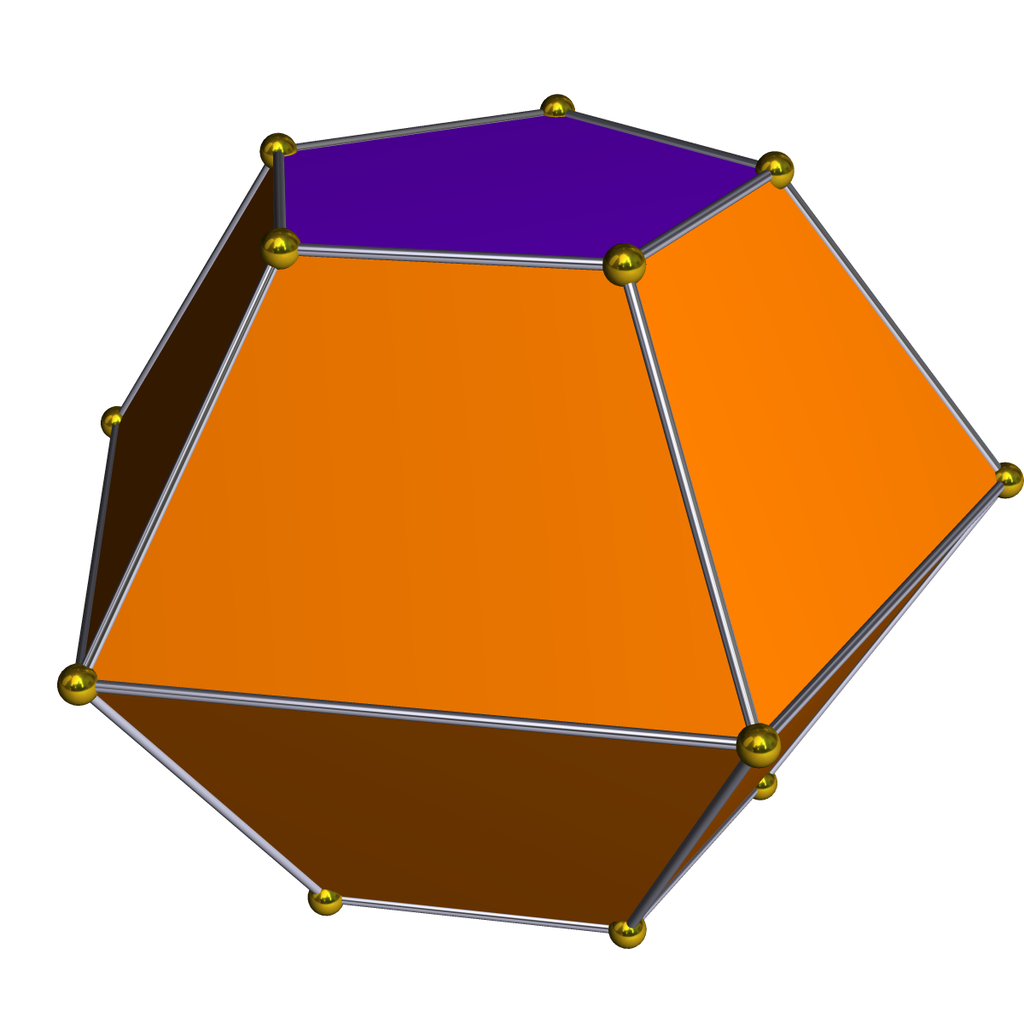圖3.雙五角錐台:10個梯形、2五邊形，對偶為雙五角錐柱

圖4.雙六角錐台: 12個梯形、2六邊形，對偶為雙六角錐柱

公式

體積公式

稜台或圓台的體積是原立體圖形的體積減去被截去部分的體積：

B₁指一個底面的面積，B₂指另一個底面的面積,andh₁，h₂指原頂點分別到兩底面的面積。考慮到：

這個體積也可用平截頭體的高h=h₂−h₁與兩底面面積的希羅平均數表達：

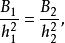
亞歷山大里亞的希羅推導出了這個公式並且憑藉它遇到了虛數。

特別地，圓台的體積是：

π等於3.14159265...，R₁,R₂是兩底面的半徑。

底面為n邊形的稜台的體積是：

a₁與a₂是底面的邊長。

表面積公式

對於一個正圓台，

LateralSurfaceArea指側面積，TotalSurfaceArea指總面積，R₁andR₂為底面半徑，s為平截頭體的斜高。一個底面為正n邊形的正稜台的表面積是：

a₁與a₂是兩底面的邊長。