設V1,V2是歐氏空間V中的兩個子空間.如果對於任意的α∈V1,β∈ V2,恆有( α,β)=0,則稱V1,V2是正交的,記作V1⊥V2。
基本介紹
- 中文名:正交子空間
- 外文名: orthogonal subspaces
- 所屬領域:數理科學
- 相關概念:正交、正交補、基本子空間等
定義
 方程(1)
方程(1)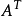
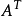
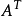
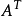

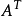





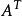
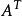

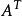
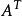
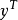
相關定理及推論




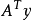


設V1,V2是歐氏空間V中的兩個子空間.如果對於任意的α∈V1,β∈ V2,恆有( α,β)=0,則稱V1,V2是正交的,記作V1⊥V2。
 方程(1)
方程(1)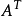
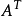
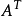
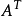

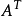





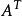
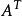

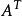
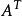
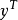




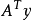

正交子空間 若內積空間中兩向量的內積為0,則它們正交。類似地,若內積空間中的向量v與子空間A中的每個向量都正交,那么這個向量和子空間A正交。若內積空間的子空間...
正交是線性代數的概念,是垂直這一直觀概念的推廣。作為一個形容詞,只有在一個確定的內積空間中才有意義。若內積空間中兩向量的內積為0,則稱它們是正交的。如果...
如果向量空間被賦予了內積,那么就可以定義正交和其它相關的概念(比如線性運算元的自伴隨性)了。在內積空間(賦予了內積的向量空間)中,有正交投影的概念。具體來說,...
7.5 正交子空間7.6 伴隨變換7.7 正交變換第8章 埃爾米特型8.1 埃爾米特型8.2 正交基底8.3 伴隨變換8.4 酉變換8.5 埃爾米特變換...
一種子空間。給定子空間按埃爾米特函式的正交子空間。設φ是域P上的線性空間V的埃爾米特函式。對埃爾米特函式而言,左、右正交是一致的。因此,若V中向量α,β的...
一、歐氏空間的概念 二、規範正交基 三、正交子空間 習題3.5 第四章 線性映射與矩陣 §4.1 線性映射的概念與基本性質 一、映射 …… 第五章 線性...
,而ri , 。那么正交子空間在 上定義一個UV空間分解 [1] :給定一個次梯度 和V分量 ,f的U-拉格朗日取決於 ,定義為:在V-空間中的相關聯的極小集是由以下公...
基於累積量增強全矢量正交子空間方法的MA建模 東大學報 2003,4。計算聽覺場景分析歷史與發展 東大學報 南大學報 2003,4。基於Hough變換的任意時頻分布線條特徵提取...
第九章 歐式空間 1. 歐式空間的定義與基本性質 2. 標準正交基、正交子空間和子空間的正交補 3. 正交矩陣與實對稱矩陣的正交化標準形 4. 正交變換、對稱變換與...
第十一章 歐氏空間§1 定義與簡單性質§2 正交基與標準正交基§3 正交子空間、正射影與最小二乘解§4 正交變換與正交方陣§5 對稱變換與對稱方陣...
、矩陣、線性空間、線性變換、多項式、特徵值、λ 矩陣、二次型和歐氏空間。...9.1歐氏空間的定義及基本性質9.2標準正交基9.3正交子空間9.4正交變換與對稱變換...
[88] 趙春暉,尤佳,李曉慧. 基於自適應核方法的正交子空間投影異常檢測算法[J]. 黑龍江大學自然科學學報. 2012(02)。[89] 王小旭,潘泉,程詠梅,趙春暉. New ...
