基本介紹
定義
推論
性質

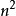
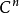

 斜埃爾米特矩陣
斜埃爾米特矩陣

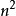
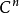

 斜埃爾米特矩陣
斜埃爾米特矩陣埃爾米特矩陣(又稱“自共軛矩陣”)是共軛對稱的方陣。埃爾米特矩陣中每一個第i 行第j 列的元素都與第j 行第i 列的元素的共軛相等。n階複方陣A的對稱單元互...
厄米特矩陣(Hermitian Matrix,又譯作“埃爾米特矩陣”或“厄米矩陣”),指的是自共軛矩陣。矩陣中每一個第i行第j列的元素都與第j行第i列的元素的共軛相等。...
埃爾米特形式(Hermite Normal form)複流形上的一種特殊雙線性形式。...... 線上性代數中,埃爾米特形式是整數Z上矩陣的簡化階梯形式的一個類似形式。就像簡化的階梯...
埃爾米特二次型是一種特殊的復二次型。對埃爾米特二次型也可以與二次型一樣地定義秩、等價和相伴的雙線性型等概念。...
反Hermite矩陣就是一個矩陣,它的共軛轉置,是它本身的負矩陣。定義:反Hermite矩陣就是一個矩陣,它的共軛轉置 是它本身的負矩陣。 [1] ...
埃爾米特(Charles Hermite,1822—1901)法國數學家。巴黎綜合工科學校畢業。曾任法蘭西學院、巴黎高等師範學校、巴黎大學教授。法蘭西科學院院士。在函式論、高等代數、...
式中Cp(x,}t)是埃爾米特矩陣,則局部放大矩陣定義為G(x,}t,s})一E(,)cPcso(二,}t ) e`a } e,式中s}=}tk,k為波數向量.[1] ...
放大矩陣是偏微分方程數值解法概念之一,指差分運算元在波數空間的等價表示。局部...式中 是埃爾米特矩陣,則局部放大矩陣定義為 ,式中 ,k為波數向量。...
埃爾米特度f空jet (Hermitian metric space)一類線性空間.指帶非退化埃爾米特函式的線性空間。...
哈密爾頓證明了4×4矩陣的情況,而一般情況下的證明是德國數學家弗羅貝尼烏斯(F.G.Frohenius)於1898年給出的[5] 。1854年時法國數學家埃爾米特(C.Hermite)使用...
么正矩陣表示的就是厄米共軛矩陣等於逆矩陣。對於實矩陣,厄米共軛就是轉置,所以...么正矩陣性質 編輯 U可逆;是酉矩陣么正矩陣參見 編輯 埃爾米特矩陣 辛矩陣 ...
3.2 ?n?階方陣的三角分解57 3.2.1 矩陣的三角分解57 3.2.2 三角分解的套用59 3.3 埃爾米特矩陣及其分解60 3.4 矩陣的最大秩分解66 ??3.5 矩陣的奇異...
埃爾米特定理是多項式最大公因式定理的推廣。設f1(x),f2(x),...,fs(x)(s≥2)是數域P上的s個非零多項式,則存在一個𝝀矩陣A(𝝀),它的第一行元素是...
在數學裡,作用於一個有限維的內積空間,一個自伴運算元(self-adjoint operator)等於自己的伴隨運算元;等價地說,表達自伴運算元的矩陣是埃爾米特矩陣。即厄米算符表達了一...
其中 和 是單位向量。 ,是正交矩陣,且detH=-1。householder變換性質 編輯 householder變換矩陣有如下性質:1)它是埃爾米特矩陣: 2)它是正交矩陣:...
