埃爾米特定理是多項式最大公因式定理的推廣。設f1(x),f2(x),...,fs(x)(s≥2)是數域P上的s個非零多項式,則存在一個𝝀矩陣A(𝝀),它的第一行元素是f1(𝝀),f2(𝝀),...,fs(𝝀),而其行列式|A(𝝀)|=(f1(𝝀),f2(𝝀),...,fs(𝝀)),此稱為埃爾米特定理。
基本介紹
- 中文名:埃爾米特定理
- 外文名:Hermitian theorem
- 適用範圍:數理科學
簡介
推論
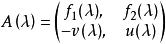
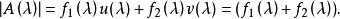
埃爾米特定理是多項式最大公因式定理的推廣。設f1(x),f2(x),...,fs(x)(s≥2)是數域P上的s個非零多項式,則存在一個𝝀矩陣A(𝝀),它的第一行元素是f1(𝝀),f2(𝝀),...,fs(𝝀),而其行列式|A(𝝀)|=(f1(𝝀),f2(𝝀),...,fs(𝝀)),此稱為埃爾米特定理。
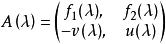
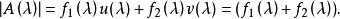
埃爾米特定理是多項式最大公因式定理的推廣。設f1(x),f2(x),...,fs(x)(s≥2)是數域P上的s個非零多項式,則存在一個𝝀矩陣A(𝝀),它的第一行元素是...
埃爾米特(Charles Hermite,1822—1901)法國數學家。巴黎綜合工科學校畢業。曾任法蘭西學院、巴黎高等師範學校、巴黎大學教授。法蘭西科學院院士。在函式論、高等代數、...
埃爾米特插值公式(Hermite interpolation formina )區域上解析函式的拉格朗日插值多項式的積分表示式。不少實際的插值問題不但要求在節點上的函式值相等,而且還要求對應...
不少實際的插值問題不但要求在節點上的函式值相等,而且還要求對應的導數值也相等,甚至要求高階導數也相等,滿足這種要求的插值多項式就是埃爾米特插值多項式。...
有唯一的埃爾米特解M,並且M是正定的。定理1和系1的含義是,若A是漸近穩定的,且N正定或半正定,則(1)式的解M必為正定,但這並不是說,若A是漸近穩定且M是...
阿貝爾定理: 1.如果冪級數在點x0處(x0不等於0)收斂,則對於適合不等式|x|<...用埃爾米特(Hermite)的話來說,“阿貝爾留下的後繼工作,夠數學家們忙上五百年...
希爾伯特-施密特定理是對稱核線性積分運算元的基本定理,是希爾伯特(Hilbert,D.)和...對稱核線性積分運算元是具有對稱核的線性積分運算元,又稱為具有埃爾米特核的線性積分...
1861年克萊布希從埃爾米特定理推導出實斜對稱矩陣的非零特徵根是純虛數。1862年他出版《彈性學教程》(Theorie der Elastizität fester Körper)。[1]...
