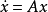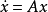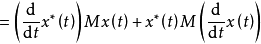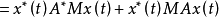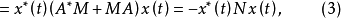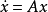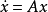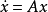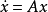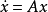基本介紹
- 中文名:李亞普諾夫定理
- 外文名:Liapunov’s theorem
- 所屬學科:數學
- 提出者:李亞普諾夫
- 簡介:關於實矩陣特徵值的一個命題
基本介紹,相關說明,
基本介紹
李亞普諾夫定理是數學生態學的重要定理之一,是判定系統穩定性質的重要定理,對於複雜生態系統

1.V(x*)=0,並且x*是V(x)在Ω內惟一整體最小值;
2.在Ω內,對每一個正值K,曲面族V(x)=K都是閉曲面;
3.導數
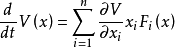
李亞普諾夫定理斷言:若系統有正平衡點x*∈Ω,如果存在李亞普諾夫函式V(x),在Ω內dV/dt是負定的,則x在區域Ω內為漸近穩定的(即以Ω內任意點為初值的解,當t→∞時趨於x*),特別當Ω≡Rn+時,x*稱為全局漸近穩定的。
相關說明
定理1(李亞普諾夫定理) A的所有特徵值都具有負實部,或等價地說,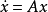 的零狀態是漸近穩定的,若且唯若對於任意給定的正定埃爾米特矩陣N,矩陣方程
的零狀態是漸近穩定的,若且唯若對於任意給定的正定埃爾米特矩陣N,矩陣方程
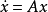

系1 A的所有特徵值都具有負實部,或等價地說,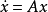 的零狀態是漸近穩定的,若且唯若對於任意給定的,具有{A,N}可觀測之性質的,半正定埃爾米特矩陣N,矩陣方程
的零狀態是漸近穩定的,若且唯若對於任意給定的,具有{A,N}可觀測之性質的,半正定埃爾米特矩陣N,矩陣方程
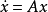
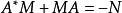
定理1和系1的含義是,若A是漸近穩定的,且N正定或半正定,則(1)式的解M必為正定,但這並不是說,若A是漸近穩定且M是正定,由(1)式算得的矩陣N是正定或半正定的。
因定理1對於任何正定埃爾米特矩陣N均成立,故(1)式中的矩陣N常選為單位矩陣,由於M是埃爾米特矩陣,故其中有n2個未知數需要求解,若M是實對稱矩陣,則其中有n(n+1)/2 個未知數需要求解。因此,矩陣方程(1)實際上包含有n2個線性代數方程,為了套用定理1,我們必須對M求解n2個方程,隨後核查M是否正定,這些工作實非易事,因此,定理1及其系一般並不用來確定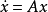 的穩定性。然而,套用李亞普諾夫第二法研究非線性時變系統的穩定性時,定理1卻是至關重要的。
的穩定性。然而,套用李亞普諾夫第二法研究非線性時變系統的穩定性時,定理1卻是至關重要的。
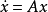
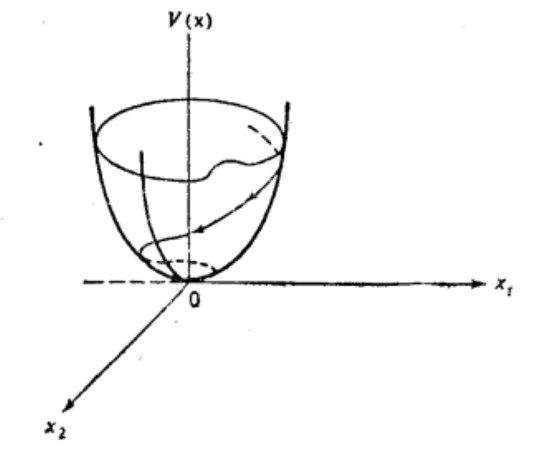
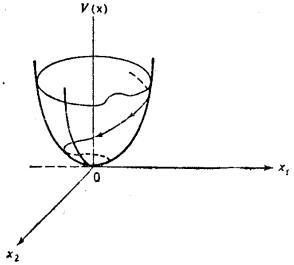 圖1 李亞普諾夫函式
圖1 李亞普諾夫函式現對李亞普諾夫定理作物理的解釋,若埃爾米特矩陣M是正定的,則
V(x) x*Mx, (2)
x*Mx, (2)

的曲面呈碗形,如圖1所示.現在構想,沿著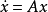 的軌跡連續求取V的值,我們想知道,隨著狀態沿軌跡移動時, V的值是增加還是減小,沿著
的軌跡連續求取V的值,我們想知道,隨著狀態沿軌跡移動時, V的值是增加還是減小,沿著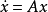 的任何軌跡取V關於t的導數,得
的任何軌跡取V關於t的導數,得