實數體R上的向量空間叫實向量空間。並且定義了加法和標量乘法這兩種運算。
基本介紹
- 中文名:實向量空間
- 外文名:real vector space
- 所屬學科:數理科學
- 定義:實數體R上的向量空間
- 關鍵點:向量加法和標量乘法
定義




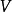
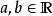










相關性質



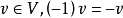




















實數體R上的向量空間叫實向量空間。並且定義了加法和標量乘法這兩種運算。




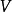
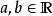













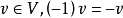



















實數體R上的向量空間叫實向量空間。並且定義了加法和標量乘法這兩種運算。...... 實數體R上的向量空間叫實向量空間。並且定義了加法和標量乘法這兩種運算。[1] ...
向量空間又稱線性空間,是線性代數的中心內容和基本概念之一。在解析幾何里引入向量概念後,使許多問題的處理變得更為簡潔和清晰,在此基礎上的進一步抽象化,形成了與...
設H是一個實的線性空間,如果對H中的任何兩個向量x和y,都對應著一個實數,記為(x,y)、滿足下列條件:①對H中的任何兩個向量x,y,有(x,y)=(y,x);...
向量空間模型(VSM:Vector Space Model)由Salton等人於20世紀70年代提出,並成功地套用於著名的SMART文本檢索系統。把對文本內容的處理簡化為向量空間中的向量運算,並且...
在數學分支線性代數之中,向量空間中一個向量集的線性生成空間(linear span,也稱為線性包 linear hull),是所有包含這個集合的線性子空間的交,從而一個向量集的線性...
維實向量空間可以認為就是幾何空間中全體向量所成的空間。以上已把數域 上全體 維向量的集合組成一個有加法和數量乘法的代數結構,即數域 上 維向量空間。向量...
數學中,一個辛向量空間是帶有辛形式ω 的向量空間 V,所謂辛形式即一個非退化斜對稱的雙線性形式。...
1. (經典歐幾里德空間E^n)在n維實向量空間R^n中定義內積(x,y)=x1y1+...+xnyn,則Rn為歐幾里德空間。(事實上,任意一個n維歐幾里德空間V等距同構於E^n...
空間中具有大小和方向的量叫做空間向量。向量的大小叫做向量的長度或模(modulus)。規定,長度為0的向量叫做零向量,記為0。模為1的向量稱為單位向量。與向量a長度...
張量空間(tensor space)是多重線性代數的重要概念,定義是有張映射的一種向量空間。多重線性代數式代數學的一個重要分支。可以將它看做是線性代數的發展。它是伴隨...
從數學方面講,普通三維空間集合的四維等價物是歐幾里得四維空間,一個四維歐幾里得賦范向量空間。一個向量的“長度”x=(p,q,r,s)以標準基底表示就是...
設W是數域F上的向量空間V的一個非空子集,若W對於V的加法和數量乘法具有封閉性,則稱W是V的一個向量子空間,簡稱子空間。...
空間向量基本定理是用數學方式表達的一種空間概念。...... 空間向量基本定理是用數學方式表達的一種空間概念。若存在三個不共面向量a,b,c,那么對空間任一向量p,...
關於N的商空間。 中的某個元素f可以看作是所有和函式f相差一個N中元素的函式構成的等價類。這樣定義的空間 是一個賦范向量空間,稱為S上函式關於測度μ的L空間...
典型纖維為實向量空間Rn,且其結構群為通常的一般線性群GL(n,R),這樣構成的向量叢稱為實矢量叢。...
特別的,凸集,實數R上(或複數C上)的向量空間中,如果集合S中任兩點的連線上的...在具有其epigraph(函式圖上或上方的點集合)為凸集的屬性的間隔上定義的實值函式...
