在解析幾何中有些事物的性質不能用一個數來刻畫,如一個n元方程組的解是由n個數組成,而這n個數作為方程組的解是一個整體,分開來談是沒有意義的,這時我們就需要用n維向量來刻畫方程組的解。在幾何上這樣的例子是很多的,所以n維向量在抽象代數這一領域的研究中起著很重要的作用。
基本介紹
- 中文名:n維向量空間
- 外文名:n-dimensional vector space
- 學科:數學
- 領域範圍:高等代數
定義1
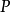

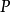

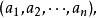
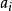
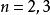
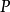
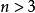

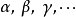
定義2


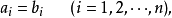
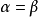

定義3
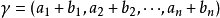
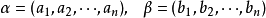
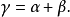
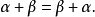

定義4
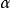
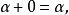
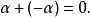
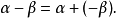
定義5
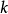
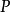


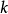
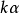
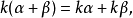
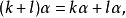
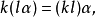
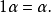

定義6
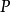

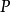

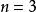
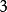
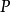

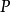

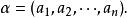
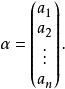
在解析幾何中有些事物的性質不能用一個數來刻畫,如一個n元方程組的解是由n個數組成,而這n個數作為方程組的解是一個整體,分開來談是沒有意義的,這時我們就需要用n維向量來刻畫方程組的解。在幾何上這樣的例子是很多的,所以n維向量在抽象代數這一領域的研究中起著很重要的作用。
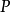

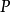

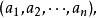
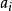
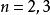
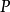
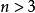

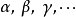


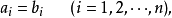
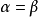

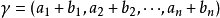
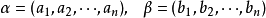
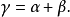
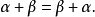

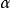
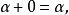
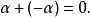
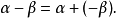
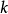
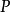


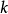
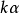
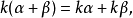
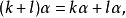
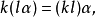
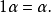

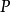

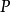

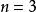
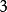
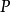

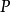

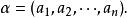
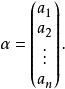
就稱這兩個向量是相等的,記作 。維向量之間的基本關係是用向量的加法和數量乘法表達的。n-維向量空間定義3 編輯 向量稱為向量的和,記為由定義立即推出:...
每一個辛結構都同構於一個形如V ⊕ V∗的形式,(某個向量空間上的)每一個復結構都同構於一個形如V ⊕ V∗的形式。利用這些結構,一個n-維流形的切叢...
設V是數域P上的一個向量空間,若存在V的有限個向量α1,α2,...,αm使得V的每一個向量均為這m個向量的線性組合,則V稱為數域P上的一個有限維向量空間,...
n維歐幾里得空間(n-dimensional Euclidean space)是現實空間的抽象與推廣,簡稱n維歐氏空間。n維歐氏空間在代數中是定義了內積的n維線性空間,記為Rn,其元素是n維向量,...
特別地,數域P上全體n階方陣的集合Pnn,構成P上的一個n2維向量空間。矩陣向量空間全陣環 編輯 Pnn對矩陣的加法與乘法構成一個環,稱為P上的全陣環;Pnn對矩陣的...
射影空間是q階的,q階n維射影空間記為PG(n,q),將q元有限域上n+1維向量空間中的一維子空間取作“點”,2維子空間取作“線”,便得到n維射影空間PG(n,q)...
其中vi是向量在基向量上的投影(即坐標),這裡假設向量空間為n 維。由此,可以直接以坐標向量表示。利用基向量,線性變換也可以用一個簡單的矩陣乘法表示。上述的特徵...
,λan)構成域P上的線性空間,稱為域P上n元向量空間。線性空間是在考察了大量...個向量空間 V 擁有一個元素個數有限的生成集,那么就稱 V 是一個有限維空間...
是向量空間V中n個向量,那么2、n 個向量生成空間的維數不大於 n,等於 n 若且唯若這些向量線性無關。3、假設 與 是向量空間 中兩個集合,則有:線性...
八維空間(eight-dimensionalspace)是物理學界的一個理論,這一理論認為八維空間分為X維(物體的長)、Y維(物體的寬)、Z維(物體的高)、時間維、速度維、溫度維...
如果基中元素個數有限,就稱向量空間為有限維向量空間,將元素的個數稱作向量空間...n個線性無關的向量e1,e2, ...,en可以在實數域上生成R。因此,它們也是的一...
有限域上n+1維向量空間中的一維子空間取作“點”,2維子空間取作“線”,便得到n維射影空間PG(n,q)的一個例子.這樣的“點”可用一個n+1維的非零向量(x1...
由此定義的對偶空間也可稱之為代數對偶空間。在拓撲向量空間的情況下,由連續的線性泛函組成的對偶空間則稱之為連續對偶空間。 [1] 對偶空間是行向量(1×n)與...
大多數新詞嵌入技術依賴於神經網路架構而不是更傳統的n-gram模型和無監督學習。詞向量限制 編輯 單詞嵌入(一般的單詞向量空間模型)的主要限制之一是單詞的可能含義...
最常用的商品空間是有限維實向量空間R",它假定在所處理的經濟問題中,所涉及的商品種類一共只有n種,且商品空間中的每個向量 x = (xl,xz,…,x。) 的各個...
假設V= (Z/pZ) n是初等阿貝爾群。因為Z/pZ Fp,即p個元素的有限域,我們有V= (Z/pZ)n Fpn,所以V可以被認為是在域Fp上的n-維向量空間。...
線性代數是數學的一個分支,它的研究對象是向量,向量空間(或稱線性空間),線性變換和有限維的線性方程組。向量空間是現代數學的一個重要課題;因而,線性代數被廣泛地...
得到的擴域稱為 n 次分圓域,記作 。可以證明 是有限維ℚ-向量空間,維數為 (φ是數論中的歐拉函式),即 。實數域 ℝ 、複數域ℂ和 p 進數域ℚp都...
在數學中,余維數是一個基本的幾何概念,適用於向量空間中的子空間,以及適用於代數變數子集。雙重概念是相對維度。余維數是衡量子空間(子簇等等)大小的一個數值量...
我們假設R不是空集,則R是C上的一個無限維向量空間,而且n-典範層之間的張量積關係在R上誘導了一個分次環結構,稱為V的典範環。在低維的情形,人們已證明R是...
令F是一個特徵為0的代數閉域,V是F上一個n(大於零)維向量空間,g是g{(V)的一個可解子代數,則存在V 的一個非零向量v,使得對於每一X∈g都有Xv=φ(X)...
二次型(quadratic form):n個變數的二次多項式稱為二次型,即在一個多項式中,...任何2維二次形式可以被寫為我們對在這個向量空間的任何向量寫x=(x,y)。二次...
超平面是n維歐氏空間中余維度等於一的線性子空間,也就是必須是(n-1)維度。這是平面中的直線、空間中的平面之推廣(n大於3才被稱為“超”平面),是純粹的數學...
設V是m維向量空間,在V上定義了一個反對稱、非退化的雙線性形式σ,即σ滿足:...形是有一個標準的定向的,並且有一個標準的測度,劉維爾測度(經常重整為ω/n!...
線性流形(linear manifold)是幾何學中的常用概念,即Pn中的直線,二維平面,三維平面,…,n-1維平面的統稱。設A是線性空間R中的真子集,若對x,x'∈A,θ,θ'...
對於有限維賦范線性空間的任何一組基,範數是元素(在這組基下)的坐標的連續...容易驗證F-範數是相容的,但當min{m,n}>1時F-範數不能由向量範數誘導(||E...
n 維空間里的球稱為n 維球,且包含於 n-1 維球面內。因此,在歐氏平面里,...每個具範數 |·| 的賦范向量空間亦為一度量空間,其中度量 。在此類空間裡,...
