Pn(C)的一個子集,若它可以表示為定義在Cn+1中一組齊次多項式公共零點的集合,則稱它為射影代數簇,簡稱代數簇,也可稱它為Pn(C)的代數子集。
基本介紹
- 中文名:射影代數簇
- 外文名:projective algebraic variety
基本介紹
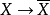
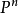
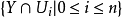
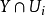
代數簇相關介紹
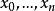
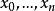

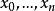
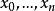

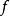
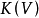
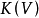
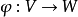
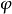
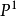
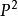
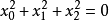
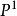
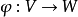
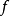
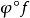
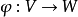
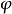
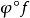
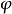
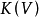
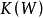
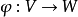
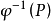
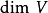

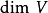


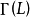
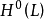
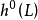
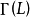
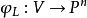

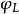
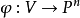
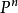
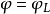
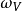
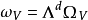

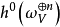
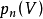
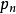
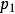
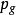
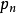
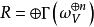
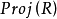
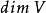

Pn(C)的一個子集,若它可以表示為定義在Cn+1中一組齊次多項式公共零點的集合,則稱它為射影代數簇,簡稱代數簇,也可稱它為Pn(C)的代數子集。
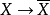
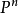
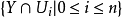
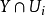
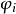
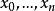
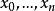

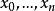
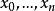

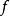
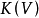
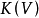
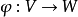
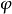
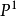
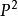
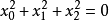
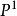
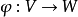
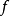
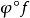
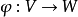
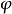
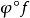
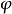
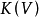
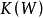
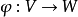
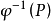
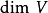

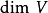


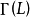
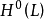
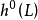
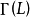
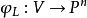

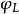
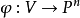
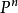
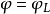
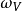
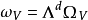

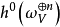
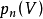
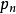
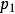
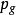
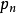
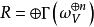
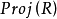
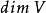
Pn(C)的一個子集,若它可以表示為定義在Cn+1中一組齊次多項式公共零點的集合,則稱它為射影代數簇,簡稱代數簇,也可稱它為Pn(C)的代數子集。...
代數幾何學上,代數簇是多項式集合的公共零點解的集合。代數簇是經典(某種程度上也是現代)代數幾何的中心研究對象。 術語簇(variety)取自拉丁語族中詞源(cognate of...
代數幾何,是現代數學的一個重要分支學科。它的基本研究對象是在任意維數的(仿射或射影)空間中,由若干個代數方程的公共零點所構成的集合的幾何特性。這樣的集合通常...
代數閉鏈是代數幾何和Hodge理論中的重要概念。在一個復 n 維的代數簇 M 中, 一條復 p 維的閉鏈 (cycle)如果可以用一些多項式方程組的零點集來定義, 就成為...
利用概型理論,P.德利涅於70年代初證明了A.韋伊關於有限域上射影代數簇ζ函式的一個著名猜想。現在,交換代數的運用已深入到微分與代數拓撲、多複變函數論、奇點...
3.6 齊次理想與射影代數簇第四章 計算實代數幾何4.1 實閉域4.2 實根隔離4.3 Tarski方法4.4 柱形代數分解4.5 實解隔離與分類5.1 Galois群與Galois擴張...
3.1 理想與代數簇3.2 理想的基本運算3.3 理想與代數簇的分解3.4 維數與Hilbert函式3.5 理想根的計算3.6 齊次理想與射影代數簇...
霍奇猜想斷言,對於所謂射影代數簇這種特別完美的空間類型來說,稱作霍奇閉鏈的部件實際上是稱作代數閉鏈的幾何部件的(有理線性)組合。...
周煒良(1911~1995), 安徽建德(今東至)人,著名華裔數學家,20世紀代數幾何學領域...阿貝爾簇都可嵌入射影空間,而周煒良則證明任何齊次簇(不必完備)也可嵌入射影...
霍奇猜想是代數幾何的一個重大的懸而未決的問題。由威廉·瓦倫斯·道格拉斯·霍奇提出,它是關於非奇異復代數簇的代數拓撲和它由定義子簇的多項式方程所表述的幾何的...
相交理論(intersection theory)是代數幾何學中最基本的理論之一。若X是n維光滑擬射影代數簇,Y和Z是X的余維數為r和s的子簇,並且Y和Z正常地相交,也就是說Y∩...
霍奇猜想斷言,對於所謂射影代數簇這種特別完美的空間類型來說,稱作霍奇閉鏈的部件實際上是稱作代數閉鏈的幾何部件的(有理線性)組合。...
代數曲面中最重要的一類除子 概念推廣 射影代數簇 目錄 1 簡介 2 可逆層 豐富除子簡介 編輯 豐富除子H就是滿足Nakai判別法的除子:HC>0, HH>0, 這裡C是...
有一個非常豐富除子的proper代數簇必定是射影代數簇,反之亦然。 這是因為相應的有理映射給出了它到射影空間的一個閉嵌入。需要注意的是,very ample invertible ...
分次環與模發展的另一動力是交換代數幾何中射影代數簇,20世紀70年代以來,由於非交換代數幾何及群表示論的推動,環論已進入一個新的階段。若環R的乘法適合交換律...
分次環與模發展的另一動力是交換代數幾何中射影代數簇,20世紀70年代以來,由於非交換代數幾何及群表示論的推動,環論已進入一個新的階段。若環R的乘法適合交換律...
這個高度的定義比較複雜,但是它可以轉化成另一個比較容易敘述的高度概念,西格爾把K上的所有g維主極化阿貝爾簇作成一個新的射影代數簇ng,叫作參量空間(moduli ...
霍奇猜想斷言,對於所謂射影代數簇這種特別完美的空間類型來說,稱作霍奇閉鏈的部件實際上是稱作代數閉鏈的幾何部件的(有理線性)組合。三、龐加萊猜想(Poincaré ...
霍奇猜想斷言,對於所謂射影代數簇這種特別完美的空間類型來說,稱作霍奇閉鏈的部件實際上是稱作代數閉鏈的幾何部件的(有理線性)組合。...
2. 霍奇猜想(Hodge Conjecture):在非奇異復射影代數簇上, 任一霍奇類是代數閉鏈類的有理線性組合。 3. 納威厄-斯托克斯方程(Navier-Stokes Equations):證明或否...
