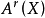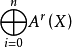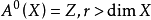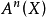相交理論(intersection theory)是代數幾何學中最基本的理論之一。若X是n維光滑擬射影代數簇，Y和Z是X的余維數為r和s的子簇，並且Y和Z正常地相交，也就是說Y∩Z的不可約分支的余維數都是r+s，則可以定義Y和Z沿著它們交集的某個不可約分支Wj上的相交重數i(Y，Z；Wj)，使得它與幾何直觀相容，然後就可定義Y和Z的相交積Y.Z為一個余維數r+s的閉鏈Y.Z=∑i(Y，Z；Wj)Wj。若Y和Z並非正常地相交，則根據周煒良的移動定理，可以找一個與Z代數等價的Z′，使得Y與Z′正常地相交，記Y·Z=Y·Z′，利用雙線性性質，就可定義任意的余維數r的閉鏈與余維數s的閉鏈的相交。這樣建立的相交理論滿足一系列公理，並使得周環得以定義。
基本介紹
- 中文名：相交理論
- 外文名：intersection theory
- 所屬學科：數學
- 所屬問題：代數幾何
- 性質：代數幾何學中最基本的理論之一
相關分析,公理介紹及證明,
相關分析
曲面上的相交論可以概括為，存在唯一的一個對稱雙線性配對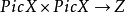
，並通過下述要求來法化，即對於兩條橫截相交的非異曲線
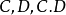恰是
與
的交點個數。證明此定理的主要工具是Bertini定理，它使我們對任意兩個除子，可以在它們的線性等價類中移動它們，使其成為橫截相交的不可約非異曲線的差。
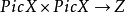
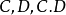
高維時的情況相當複雜，相應的活動引理顯得弱了一些，所以需要一個較強的法化要求。結果發現展開相交理論的最適當的方式原來是同時對所有的簇都進行討論，連態射
的相伴函子式映射
及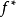
，也作為結構部分被包括進去。
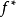
設X為k上任意簇，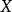
上一個余維r的環元，是指X的余維r的閉不可約子簇生成的自由Abel群中的一個元。故可將一個環元寫為
，
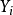為子簇，
。有時要論及一個有用的概念，即與閉子概型相伴的環元。設Z是余維r的閉子概型，
是Z的所有餘維r的不可約分支，定義
為相伴於Z的環元，其中
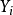是Z在的廣點
的局部環
的長度。
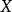
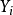
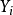
設為簇間的態射，Y為X的子簇．如果
，令
，如果
，則函式域
是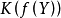
的有限擴張域，令
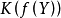
由線性擴張便定了X上環元的群到X'上環元的群的同態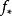
。
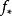
現在來定義有理等價性，當
是
上線性等價的Weil除子時，稱
為X上有理等價的環元。一般的情形，對所有的子簇V，及所有上線性等價的Weil除子讓
生成了等價關係。在這個等價關係下，我們定義了X上環元的有理等價性。特別地，當X本身是正規時，余維l的環元的有理等價性與Weil除子的線性等價性一致。
在一個給定的簇類
上，一個相交理論由對每個
及每個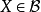
給出一個配對
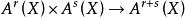構成，這些配對應滿足下面列m的公理。如果
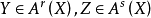，我們以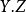
表示其相交環元類。
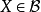
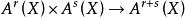
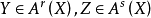
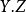
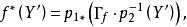
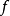
上述諸元必須滿足下列要求。
A1. 相交配對使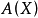
對每個
成為一個交換的可結合分次環，並具麼元，稱為X的周環。
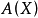
A2. 對中簇的任意態射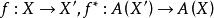
是環同態，如
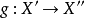是另一態射，則
。
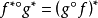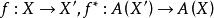
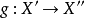
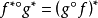
A3. 對中簇的任意本徵態射
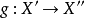是分次群同態(移動了分次)，如果是另一個態射，則
。
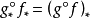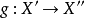
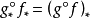
A4. 投射公式。若是本徵態射，
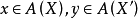，則
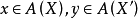
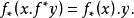
A5. 化為對角線。如果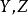
為X上環元，
為對角態射，則
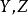
A6. 局部特性。如果Y與Z是X的子簇，它們正常相交(即
的每個不可約分支的余維等於
)，則可記
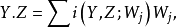
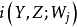
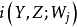
A7. 法化。設Y是X的子簇，Z是與Y正常相交的有效Cartier除子，則
恰好是Y上Cartier除子相伴的環元，其中在Y上是由Z的局部方程限制在Y上定義的子概型。(它特別表明，橫截相交的非異子簇的重數為1)。
公理介紹及證明
定理1 設是某給定代數閉域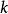
上非異擬射影簇的類，則對簇
上的有理等價環元類，有一個唯一的相交理論，滿足上面的A1-A7公理。
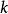
證明：定理的證明中有兩個主要的成分。一個是局部相交重數的正確定義；另一個是周煒良的活動引理。有許多方式來定義相交重數。我們只提出Serre的定義，從歷史的觀點說它是最近的，然而卻有緊湊簡潔的好處。如果
正常相交，W為的一個不可約分支，定義
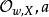
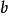
另一個成分是周煒良活動引理，它說的是，如果是非異擬射影簇X上的環元，則存在一個有理等價於Z的環元Z'，使得Y與Z'正常相交。另外，如果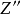
是另一個這種環元，則
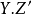與
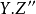有理等價。
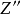
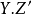
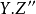
相交理論唯一性的證明如下： 給出X上環元，由活動引理知道，可以假定它們正常相交，於是利用化為對角線(A5)，我們可化為在
上計算
的情形。它的好處在於△是個局部完全交。因為相交重數是局部的，我們可以化到其中一個環元為Cartier除子的完全交情形。於是，重複套用法化條件(A7)便給出了唯一性。
