初等阿貝爾群

在群論中，初等阿貝爾群是有限阿貝爾群，這裡的所有非平凡元素都有 p 階而 p 是素數。

基本介紹

• 中文名：初等阿貝爾群
• 定義：有限阿貝爾群
• 性質：所有非平凡元素都有p階
• 學科：群論
• 領域：群論

介紹

在群論中，初等阿貝爾群是有限阿貝爾群，這裡的所有非平凡元素都有p階而p是素數。

通過有限生成阿貝爾群的分類，所有初等阿貝爾群必定有如下形式

• (Z/pZ)ⁿ.
  

對於非負整數n。這裡的Z/pZ指示p階的循環群(或等價的整數模以p)，而冪符號表示意味著n元笛卡爾積。

例子和形式

• 初等阿貝爾群 (Z/2Z) ²有四個元素: { [0,0], [0,1], [1,0], [1,1] }。加法是逐分量進行，結果要模以 2。例如，[1,0] + [1,1] = [0,1]。
  
• (Z/pZ) ⁿ由n個元素生成，而n是最小的可能的生成元數目。特別是集合 {e₁, ...,e_n} 這裡的e_i在第i個分量中為 1 而在其他地方為 0 是極小生成集合。
  
• 所有初等阿貝爾群都有非常簡單的有限展示:
  

(Z/pZ)ⁿ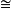<e₁, ...,e_n|e_i= 1,e_ie_j=e_je_i>.

向量空間結構

假設V= (Z/pZ) ⁿ是初等阿貝爾群。因為Z/pZF_p，即p個元素的有限域，我們有V= (Z/pZ)ⁿF_pⁿ，所以V可以被認為是在域F_p上的n-維向量空間。

讀者可能發現 F_pⁿ有比群V更大的結構，特別是它除了(向量/群)加法之外還有標量乘法。但是V作為阿貝爾群有唯一一個Z-模結構，這裡的Z的作用對應於重複的加法，而這個Z-模結構一致於F_p標量乘法。就是說，c·g=g+g+...+g(c次) 這裡的c在F_p中(考慮為整數帶有 0≤c<p) 給予V一個自然的F_p-模結構。

自同構群

作為向量空間V有如例子中那樣的基{e₁, ...,e_n}。如果我們選取 {v₁, ...,v_n} 為任何V的n個元素，則通過線性代數我們有映射T(e_i) =v_i唯一擴張為 V 的線性變換。每個這種 T 都可以被認為是從V到V的群同態(自同態)並同V的任何自同態一樣可以被認為是V作為向量空間的線性變換。

如果我們限制注意力於V的自同構，我們有 Aut(V) = {T:V->V| kerT= 0 } = GL_n(F_p)，即在 F_p上的n×n可逆矩陣的一般線性群。