基本介紹
- 中文名:球形
- 外文名:sphere
- 特點:球心到球面上的距離都相等
- 舉例:保齡球
- 簡稱:球
- 領域:數學;幾何
簡介
性質
歐氏空間裡的球形











1.體積







一般度量空間裡的球形






賦范向量空間裡的球
1.p-範數

2.一般凸範數




拓撲空間裡的球形
1.開集


2.拓撲球



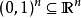









生活中常見球形
數學中的球形







































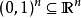













球形(球形是日常生活中人們的叫法,嚴格的來說叫做球體,英文:sphere)是一種簡單空間幾何體。半圓以它的直徑為旋轉軸,旋轉所成的曲面叫做球面。球面所圍成的幾何體...
球形彎頭也稱轉向球,在水泥及生料的氣力輸送系統中,作為管道彎頭的代用件,以其製作簡單,安裝方便,耐用性能好等優點,在大中型水泥廠的氣力輸送中套用日益廣泛。...
球形壓力容器可用以貯存各種氣體、液化石油氣、液化天然氣、液態烴、液氨、液氮、液氧和液氫等。...
球形容器又稱球罐,殼體呈球形。是貯存和運輸各種氣體、液體、液化氣體的一種有效、經濟的壓力容器。...
球形支座是指盆式橡膠支座的基礎上發展起來的一種新型橋樑支座。球形支座有固定支座、單向活動支座和多向活動支座之分。由於球形支座不再使用橡膠承壓,不存在橡膠變...
與物體相同體積的球體的表面積和物體的表面積的比。球的球形度等於1,其它物體球形度小於1 ...
建築科技人員經過測定證明,球形建築物的結構,要比其他形狀建築物牢固。...... 建築科技人員經過測定證明,球形建築物的結構,要比其他形狀建築物牢固。因為,圓頂建築物...
球形活性炭(Spherical Active Carbon, SAC)體形結構為至少含有一層由活性炭材料製成的球形外殼,球形外殼內是球形核心體,可由不同於球形外殼材料的無機材料製作,...
止回閥又稱為逆流閥、逆止閥、背壓閥、單向閥。這類閥門是靠管路中介質本身的流動產生的力而自動開啟和關閉的,屬於一種自動閥門。球形止回閥是一種採用多球、多...
球形透鏡是一種重要的光學元件,主要由光學玻璃等材料製成,用於光纖之間、雷射與光纖之間以及光纖與探測器之間的耦合,或者用於薄膜過濾密集波分復用器中光纖光束的準...
球形門鎖:內、外執手(鎖柄)為球形,用於安裝在木門、鋼門、鋁合金門及塑膠門上使用的門鎖。...
球形念珠藻,是念珠藻科、念珠藻屬藻類植物,分布於湖南,江西,廣西。...... 球形念珠藻,是念珠藻科、念珠藻屬藻類植物,分布於湖南,江西,廣西。中文學名 球形念珠...
球形機器人:機器人球形機器人:《刺蝟索尼克》系列的角色...... 球形機器人:機器人 球形機器人:《刺蝟索尼克》系列的角色 V百科往期回顧 新手上路 成長任務 編輯入...
球形風化是岩石出露地表接受風化時,由於稜角突出,易受風化,故稜角逐漸縮減,最終趨向球形的風化過程,外文名是The spherical weathering。...
球形元件是在球床高溫氣冷堆上使用的燃料元件。由德國研究和發展,其主要特點就是利用球的流動性,實現不必停堆就能完成裝卸料。球形燃料元件主要有注塑型元件、壁紙...
球形機器人是指一類驅動系統位於球殼(或球體)內部,通過內驅動方式實現球體運動的機器人,研製了三種不同結構形式的、可安裝視覺相機的球形移動機器人樣機:BHQ-1、...
球形封頭(qiuxingfengtou)也稱為球型封頭,是以球殼的球冠部分所形成的封頭,有半球形封頭和無折邊球性封頭兩類。
LED球形燈是替代傳統白熾燈泡的新型節能燈具。傳統白熾燈(鎢絲燈)耗能高、壽命短,在全球資源緊張的大環境下下,已漸漸被各國政府禁止生產,隨之替代產品是電子節能燈...
球形閃電又稱電光火球。球形閃電並不是閃電,它與閃電幾乎沒有相同之處,所以把這種現象命名為“球形閃電”是不準確的,應當命名球形閃電為“電光火球”,即與電磁場...
岩石出露地表接受風化時,由於稜角突出,易受風化(角部受三個方向的風化,棱邊受兩個方向的風化,而面上只受一個方向的風化),故稜角逐漸縮減,最終趨向球形。這樣的...
仙人球是外形呈球狀的仙人掌科多肉植物的統稱,仙人峰為灌叢狀肉質植物,有很多品種。它們的原生地多為沙漠地帶,喜高溫乾旱氣候。莖呈球形或橢圓形,綠色,花著生於縱...
